Models

knitr::opts_chunk$set(cache = FALSE, fig.retina = 2,
                      tidy.opts = list(width.cutoff = 120),  # For code
                      options(width = 120))  # For output

library(tidyverse)
library(stringr)
library(forcats)
library(stargazer)
library(huxtable)
library(lme4)
library(modelr)
library(broom)
library(broom.mixed)
library(scales)
library(formula.tools)
library(here)

source(here("lib", "graphics.R"))
source(here("lib", "pandoc.R"))
source(here("lib", "bayes.R"))

source(here("lib", "robustness_models_definitions.R"))
source(here("lib", "h1_model_definitions.R"))
source(here("lib", "h2_model_definitions.R"))
source(here("lib", "h3_model_definitions.R"))

my.seed <- 1234
set.seed(my.seed)

df.country.aid <- readRDS(here("Data", "data_clean",
                               "df_country_aid_no_imputation.rds"))

df.country.aid.impute <- readRDS(here("Data", "data_clean",
                                      "df_country_aid_imputation.rds"))

df.country.aid.impute.m10 <- readRDS(here("Data", "data_clean",
                                          "df_country_aid_imputation_m10.rds"))

dcjw.questions.clean <- read_csv(here("Data", "data_manual", "dcjw_questions.csv"))
dcjw.responses.clean <- read_csv(here("Data", "data_manual", "dcjw_responses.csv"))

# Load clean coefficient names and append "within" and "between" to them,
# resulting in a giant table of possible coefficient names
coef.names <- read_csv(here("Data", "data_manual", "coef_names.csv"))

coef.names.within <- coef.names %>%
  mutate(term = paste0(term, "_within"),
         term_plot = paste0(term_clean, "\n(within)"),
         term_plot_short = term_clean,
         term_clean = paste0(term_clean, "~within~"))

coef.names.between <- coef.names %>%
  mutate(term = paste0(term, "_between"),
         term_plot = paste0(term_clean, "\n(between)"),
         term_plot_short = paste0(term_clean, ""),
         term_clean = paste0(term_clean, "~between~"))

coef.names.all <- bind_rows(coef.names, coef.names.within, coef.names.between) %>%
  mutate_at(vars(term_plot, term_plot_short),
            funs(ifelse(is.na(.), term_clean, .))) %>% 
  mutate(term_plot_short = recode(term_plot_short,
                                  `Civil society reg. env. (CSRE)` = "CSRE"))

# Load clean model names
model.names <- read_csv(here("Data", "data_manual", "model_names.csv"))


# Combine original data and imputed data so calculations can happen at the same time
df.country.aid.both <- bind_rows(df.country.aid, df.country.aid.impute)

# Combine m=10 imputed data too since we use it in some robustness checks.
# Imputations 6-10 are later removed
df.country.aid.all <- bind_rows(df.country.aid, df.country.aid.impute.m10)

# All the missing values have been taken care of, but final years for leaded
# variables *are* still missing (i.e. there's no aid data for 2014, so
# total.oda_log_next_year will be NA in 2013). For this fancy random effects
# regression to work, the demeaned variables have to be based on the means of
# all rows included in the regression, so they can't include rows that are
# dropped because of missingness. This means we have to make separate demeaned
# datasets for *_after_2 and *_after_5, but ¯\_(ツ)_/¯
df.country.aid.demean.next_year.all <- df.country.aid.all %>%
  filter(!is.na(total.oda_log_next_year)) %>%
  group_by(m, cowcode) %>%
  mutate_at(vars(barriers.total, advocacy, entry, funding, 
                 polity, gdp.capita_log, gdp.capita, trade.pct.gdp, corruption, csre,
                 total.oda_log),
            funs(between = mean(., na.rm = TRUE),  # meaned
                 within = . - mean(., na.rm = TRUE))) %>%  # demeaned
  ungroup()

df.country.aid.us.demean.next_year.all <- df.country.aid.all %>%
  filter(!is.na(prop.ngo.dom_logit_next_year)) %>%
  filter(year > 1999) %>%
  group_by(m, cowcode) %>%
  mutate_at(vars(barriers.total, advocacy, entry, funding, 
                 polity, gdp.capita_log, gdp.capita, trade.pct.gdp, corruption, csre,
                 total.oda_log),
            funs(between = mean(., na.rm = TRUE),  # meaned
                 within = . - mean(., na.rm = TRUE))) %>%  # demeaned
  ungroup()

# Divide demeaned data into separate data frames: original, imputed (m=5), and imputed (m=10)
df.country.aid.demean.next_year.both <- 
  filter(df.country.aid.demean.next_year.all, !(m %in% paste0("imp", 6:10)))

df.country.aid.demean.next_year <- 
  filter(df.country.aid.demean.next_year.all, m == "original")

df.country.aid.us.demean.next_year.both <- 
  filter(df.country.aid.us.demean.next_year.all, !(m %in% paste0("imp", 6:10)))

df.country.aid.us.demean.next_year <- 
  filter(df.country.aid.us.demean.next_year.all, m == "original")

df.country.aid.demean.next_year.impute <- 
  filter(df.country.aid.demean.next_year.all, 
         m != "original", !(m %in% paste0("imp", 6:10)))

df.country.aid.demean.next_year.impute.m10 <- 
  filter(df.country.aid.demean.next_year.all, m != "original")

# Demean data with total.oda_log leaded by 2 years and 5 years
# After 2 years
df.country.aid.demean.after_2.both <- df.country.aid.both %>%
  filter(!is.na(total.oda_log_after_2)) %>%
  group_by(m, cowcode) %>%
  mutate_at(vars(barriers.total, advocacy, entry, funding, 
                 polity, gdp.capita_log, gdp.capita, trade.pct.gdp, corruption, csre,
                 total.oda_log),
            funs(between = mean(., na.rm = TRUE),  # meaned
                 within = . - mean(., na.rm = TRUE))) %>%  # demeaned
  ungroup()

df.country.aid.demean.after_2 <- 
  filter(df.country.aid.demean.after_2.both, m == "original")

df.country.aid.demean.after_2.impute <- 
  filter(df.country.aid.demean.after_2.both, m != "original")

# After 5 years
df.country.aid.demean.after_5.both <- df.country.aid.both %>%
  filter(!is.na(total.oda_log_after_5)) %>%
  group_by(m, cowcode) %>%
  mutate_at(vars(barriers.total, advocacy, entry, funding, 
                 polity, gdp.capita_log, gdp.capita, trade.pct.gdp, corruption, csre,
                 total.oda_log),
            funs(between = mean(., na.rm = TRUE),  # meaned
                 within = . - mean(., na.rm = TRUE))) %>%  # demeaned
  ungroup()

df.country.aid.demean.after_5 <- 
  filter(df.country.aid.demean.after_5.both, m == "original")

df.country.aid.demean.after_5.impute <- 
  filter(df.country.aid.demean.after_5.both, m != "original")

library(furrr)
plan(multiprocess)

# Print correct huxtable table depending on the type of output.
#
# Technically this isn't completely necessary, since huxtable can output a
# markdown table, which is ostensibly universal for all output types. However,
# markdown tables are inherently limited in how fancy they can be (e.g. they
# don't support column spans), so I instead let the regression table use
# huxtable's fancy formatting for html and PDF and markdown everywhere else.
if (isTRUE(getOption('knitr.in.progress'))) {
  file_format <- rmarkdown::all_output_formats(knitr::current_input())
} else {
  file_format <- ""
}

print_hux <- function(x) {
  if ("html_document" %in% file_format) {
    print_html(x)
  } else if ("pdf_document" %in% file_format) {
    print_latex(x)
  } else if ("word_document" %in% file_format) {
    print_md(x)
  } else {
    print(x)
  }
}

stars <- function(p) {
  out <- symnum(p, cutpoints = c(0, 0.01, 0.05, 0.1, 1),
                symbols = c("***", "**", "*", ""))
  as.character(out)
}

fixed.digits <- function(x, digits = 2) {
  formatC(x, digits = digits, format = "f")
}

# Use 2 significant digits only on the decimal part of the number, ignoring the
# integer part. See my question here: http://stackoverflow.com/q/43050903/120898
# fixed.digits <- function(x, digits = 2) {
#   as.character(floor(x) + signif(x %% 1, digits))
# }

# Inverse logit, with the ability to account for adjustments
# via http://stackoverflow.com/a/23845527/120898
inv.logit <- function(f, a) {
  a <- (1 - 2 * a)
  (a * (1 + exp(f)) + (exp(f) - 1)) / (2 * a * (1 + exp(f)))
}

# Take apart the pieces of a random effects formula and rebuild it
build.formula <- function(DV, IVs) {
  terms.all <- attr(terms(IVs), "term.labels")
  terms.fixed <- terms.all[!stringr::str_detect(terms.all, "\\|")]
  terms.rand <- sapply(findbars(formula(IVs)),function(x) paste0("(", deparse(x), ")"))
  
  reformulate(c(terms.fixed, terms.rand), response = DV)
}

get.rhs <- function(x) rhs.vars(x) %>% str_replace_all("1 \\| ", "")
get.lhs <- function(x) lhs.vars(x)
is_scaled <- function(x) "scaled:scale" %in% names(attributes(x))
get_scale <- function(x) attr(x, "scaled:scale")


# Meld a bunch of imputed models
meld.imputed.models <- function(model.data, exponentiate = FALSE) {
  models.df <- model.data$glance[[1]]$df.residual
  
  models.tidy <- model.data %>%
    select(tidy) %>%
    unnest(.id = "imputation")
  
  just.estimates <- models.tidy %>% 
    filter(group == "fixed") %>%
    select(imputation, term, estimate) %>%
    spread(term, estimate) %>%
    select(-imputation)
  
  just.ses <- models.tidy %>%
    filter(group == "fixed") %>%
    select(imputation, term, std.error) %>%
    spread(term, std.error) %>%
    select(-imputation)
  
  # If no imputed data was passed in, use the actual estimates and SEs
  if (nrow(just.estimates) > 1) {
    melded <- Amelia::mi.meld(just.estimates, just.ses)
  } else {
    melded <- list(q.mi = just.estimates, se.mi = just.ses)
  }
  
  melded.tidy <- as.data.frame(cbind(t(melded$q.mi), 
                                     t(melded$se.mi))) %>%
    magrittr::set_colnames(c("estimate", "std.error")) %>%
    mutate(term = rownames(.)) %>%
    select(term, everything()) %>%
    mutate(statistic = estimate / std.error,
           conf.low = estimate + std.error * qt(0.025, models.df),
           conf.high = estimate + std.error * qt(0.975, models.df),
           p.value = 2 * pt(abs(statistic), models.df, lower.tail = FALSE),
           stars = stars(p.value))
  
  if (exponentiate) {
    # Convert SEs to odds ratios. This isn't entirely 100% accurate, since the
    # melded coefficient variances (i.e. diag(vcov(.))) are just averaged, not
    # melded with Amelia's fancy mi.meld(), but ¯\_(ツ)_/¯
    #
    # https://www.andrewheiss.com/blog/2016/04/25/convert-logistic-regression-standard-errors-to-odds-ratios-with-r/
    fixed.coefs.var <- model.data %>%
      mutate(var.diag = model %>% map(~ diag(vcov(.)))) %>%
      select(var.diag, model) %>% unnest(var.diag)
    
    just.var <- models.tidy %>%
      filter(group == "fixed") %>%
      select(imputation, term) %>%
      bind_cols(fixed.coefs.var) %>%
      group_by(term) %>%
      summarise(var.diag = mean(var.diag))
    
    melded.tidy <- melded.tidy %>%
      left_join(just.var, by = "term") %>%
      mutate(or = exp(estimate),
             or.se = sqrt(or^2 * var.diag),
             or.upper = or + (qnorm(0.975) * or.se),
             or.lower = or + (qnorm(0.025) * or.se))
  }
  
  melded.tidy
}

# Expects a data frame with a column named tidy.melded and a row for model
# names. Term names are based on the first model in the data column for each
# row, and are filtered through stargazer to get the correct row order.
stargazer.fake <- function(df, caption = NULL, note = NULL, exponentiate = FALSE) {
  # Create a blank row with a bolded row name
  header.row <- function(header) {
    data_frame(term = paste0("**", header, "**"), 
               models = df$model.name, value = "") %>%
      spread(models, value)
  }
  
  note.row <- function(note) {
    crossing(term = note,
             models = df$model.name, value = "") %>%
      spread(models, value) %>%
      # Sort based on original note order
      slice(match(note, term))
  }
  
  coef.order.models <- df %>%
    # Select just the first row of each model
    unnest(data) %>%
    # Sometimes there are duplicate column names
    # magrittr::set_colnames(make.unique(colnames(.))) %>%
    # Keep order of model.name
    mutate(model.name = ordered(fct_inorder(model.name))) %>%
    group_by(model.name) %>%
    slice(1) %>% ungroup() %>%
    select(model) %>% as.list()
  
  # Use stargazer to get the coefficient order. I tried recreating stargazer's
  # coefficient ordering algorithm but it's way too complicated. So instead, we
  # cheat and let stargazer do the heavy lifting, save the output to a string,
  # and then extract the coefficient names with str_extract. Super super hacky,
  # but it works.
  #
  # See http://stackoverflow.com/a/41801861/120898
  capture.output({
    stargazer.coefs <- stargazer::stargazer(coef.order.models, 
                                            type = "text", table.layout = "t")
  }, file = "/dev/null")
  
  coef.order <- setdiff(stringr::str_extract(stargazer.coefs, "^[\\w\\.]*"), c(""))
  
  # Fixed parts
  fixed.tidy <- df %>%
    unnest(tidy.melded)
  
  if (exponentiate) {
    fixed.coefs <- fixed.tidy %>%
      mutate(fancy = paste0(fixed.digits(or, 3),
                            stars, "\\ \n(",
                            fixed.digits(or.se, 3),
                            ")"))
  } else {
    fixed.coefs <- fixed.tidy %>%
      mutate(fancy = paste0(fixed.digits(estimate, 3),
                            stars, "\\ \n(",
                            fixed.digits(std.error, 3),
                            ")"))
  }
  
  fixed.coefs <- fixed.coefs %>%
    select(model.name, term, fancy) %>%
    spread(model.name, fancy, fill = "") %>%
    # Clean up term names
    mutate(term = stringr::str_replace(term, "TRUE$|FALSE$", ""),
           term = recode(term, `(Intercept)` = "Constant")) %>%
    # Use stargazer's coefficient order
    mutate(term = factor(term, levels = coef.order, ordered = TRUE)) %>%
    arrange(term) %>%
    mutate(term = as.character(term)) %>%
    left_join(coef.names.all, by = "term") %>%
    mutate(term_clean = ifelse(term == "Constant", "Constant", term_clean)) %>%
    select(-term) %>% rename(term = term_clean) %>%
    select_(.dots = c("term", df$model.name))
  
  # Random parts
  random.coef.order.raw <- df %>%
    unnest(data) %>%
    # unnest(data) %>% magrittr::set_colnames(make.unique(colnames(.))) %>%
    select(model.name, model) %>%
    mutate(ranef = model %>% map(~ as.data.frame(VarCorr(.)))) %>%
    unnest(ranef)
  random.coef.order <- c(setdiff(unique(random.coef.order.raw$grp), "Residual"), "Residual")
  
  random.coefs <- df %>%
    unnest(data) %>%
    unnest(tidy) %>%
    filter(group != "fixed") %>%
    rename(term.raw = term, term = group) %>%
    group_by(model.name, term) %>%
    summarise(avg.random.sd = mean(estimate),
              sd.random.sd = sd(estimate)) %>%
    mutate(fancy = paste0(fixed.digits(avg.random.sd, 3),
                          "\\ \n(",
                          ifelse(is.na(sd.random.sd), "NA", fixed.digits(sd.random.sd, 3)),
                          ")")) %>%
    select(model.name, term, fancy) %>%
    spread(model.name, fancy, fill = "") %>%
    mutate(term = factor(term, levels = random.coef.order, ordered = TRUE)) %>%
    arrange(term) %>% mutate(term = as.character(term)) %>%
    left_join(coef.names.all, by = "term") %>%
    mutate(term_clean = ifelse(term == "Residual", 
                               "Residual random error ($\\sigma$)", term_clean)) %>%
    select(-term) %>% select(term = term_clean, everything())
  
  # Create the bottom half of the table
  # Calculate the average log likelihood for all imputed models
  avg.loglik <- df %>%
    unnest(data) %>% unnest(glance) %>%
    group_by(model.name) %>%
    summarise(avg.loglik = as.character(round(mean(logLik), 2))) %>%
    mutate(term = "Log likelihood (mean)") %>%
    spread(model.name, avg.loglik)
  
  # Imputation frames
  n.obs <- df %>%
    unnest(data) %>%
    mutate(n = model %>% map_int(~ nrow(.@frame))) %>%
    select(model.name, n) %>%
    group_by(model.name) %>% slice(1) %>% ungroup() %>%
    mutate(term = "Observations",
           n = scales::comma(n)) %>%
    spread(model.name, n)
  
  n.m <- df %>%
    mutate(m.new = data %>% map_int(~ nrow(.))) %>%
    select(model.name, m.new) %>% 
    mutate(m.new = ifelse(m.new == 1, 0, m.new),
           m.new = as.character(m.new)) %>%
    mutate(term = "Imputed datasets (*m*)") %>%
    spread(model.name, m.new)
  
  bottom.details <- bind_rows(n.obs, avg.loglik, n.m)
  
  if (exponentiate) {
    fixed.title <- "Fixed part (odds ratios)"
    random.title <- "Random part (original coefficients)"
  } else {
    fixed.title <- "Fixed part"
    random.title <- "Random part"
  }
  
  if (!is.null(note)) {
    notes <- bind_rows(header.row("Notes"), note.row(note))
  } else {
    notes <- NULL
  }
  
  nice.top.bottom <- bind_rows(header.row(fixed.title), fixed.coefs, 
                               header.row(random.title), random.coefs,
                               header.row("Model details"), bottom.details,
                               notes) %>%
    select_(.dots = c("term", df$model.name))
  
  # Make column names (1), (2), etc.
  # TODO: Allow for custom column names
  colnames(nice.top.bottom) <- c(" ", paste0("(", 1:length(df$model.name), ")"))
  
  # All columns are centered except the first
  # TODO: MAYBE: Let this be user configurable
  table.align <- paste0(c("l", rep("c", length(df$model.name))), collapse = "")
  
  pandoc.table.return(nice.top.bottom, keep.line.breaks = TRUE,
                      justify = table.align, caption = caption)
}

Dependent variables

As explained in each section below, we have to transform and operationalize the dependent variable (foreign aid) in different ways for each hypothesis. The table belows summarizes each simplified model specification.

\[ \begin{aligned} \boldsymbol{H_1}&: ln( \text{ODA}_{\text{OECD}} )_{i, t+1} &= \text{NGO legislation}_{it} + \text{controls}_{it} \\ \boldsymbol{H_2}&: ln( \frac{\text{contentious ODA}_{\text{OECD}}}{\text{noncontentious ODA}_{\text{OECD}}} )_{i, t+1} &= \text{NGO legislation}_{it} + \text{controls}_{it} \\ \boldsymbol{H_3}&: ln( \frac{\text{Aid to (domestic or foreign) NGOs}_{\text{USAID}}}{\text{Aid to other channels}_{\text{USAID}}} )_{i, t+1} &= \text{NGO legislation}_{it} + \text{controls}_{it} \end{aligned} \] {#eq:all-models-dvs}

General model specifications and controls

We use a standard set of controls in each model (explained in more detail here):

Democracy: polity
Wealth: gdp.capita_log (logged so it’s on the same scale as the other variables)
Government capacity: corruption
Bad stuff: internal.conflict.past.5 and natural_disaster.occurrence

Following Bell and Jones (2015), we use crossed random effects for country and year and use a combination of meaned and demeaned versions of each continuous variable to estimate both the within and between effects of each variable.

\[ y_{i, t + 1} = \beta_0 + \beta_1 (x_{it} - \bar{x}_i) + \beta_2 \bar{x}_i + \ldots \]

This approach has multiple benefits. The coefficients for the demeaned variables are roughly equivalent to their corresponding coefficients in a fixed effects model, but a fixed effects model assumes that the between effect (captured by the mean variables) is 0, which is not the case. A random effects model specified in this manner is more interpretable, as it clearly separates the within and between effects (again, within = demeaned, between = mean).

Here’s proof of how it works in some simple models. Model 1 is a basic OLS with country fixed effects. Model 2 is a basic OLS with country random effects, but potentially misspecified, since the between and within effects are conflated. Model 3 is a basic OLS with country random effects specified with between (mean; \(\bar{x}_i\)) and within (demeaned; \(x_{it} - \bar{x}_i\)) coefficients. The demeaned/within coefficients in Model 3 are identical to the fixed effects coefficients in Model 1. If rows had been dropped because of listwise deletion (like, if there were missing values in one of independent variables), the coefficients would be slightly off, since the demeaned values would have been based on group means that included the values that were dropped (e.g. all 2013 rows are dropped because of lags, but the group means included 2013). This isn’t a problem in these reduced models, but that’s one reason we impute all the data—we need the data to be as complete as possible to get the most accurate random effects.

mod.test.fe <- lm(total.oda_log_next_year ~ barriers.total + polity + 
                    as.factor(cowcode),
                  data = df.country.aid.demean.next_year)

mod.test.re <- lmer(total.oda_log_next_year ~ barriers.total + polity + 
                      (1 | cowcode),
                    data = df.country.aid.demean.next_year)

mod.test.re.fancy <- lmer(total.oda_log_next_year ~ 
                            barriers.total_between + barriers.total_within +
                            polity_between + polity_within + 
                            (1 | cowcode),
                          data = df.country.aid.demean.next_year)

# Make named list of coefficients to include in the table
all_coefs <- data_frame(model = list(mod.test.fe, mod.test.re, mod.test.re.fancy)) %>% 
  mutate(tidy = model %>% map(tidy)) %>% 
  unnest(tidy) %>% 
  filter(!str_detect(term, "cowcode"), (effect != "ran_pars" | is.na(effect))) %>% 
  filter(!duplicated(term, fromLast = TRUE)) %>% 
  filter(term != "(Intercept)") %>% 
  left_join(coef.names.all, by = "term")
  
coefs_named <- all_coefs %>% pull(term) %>% 
  set_names(all_coefs$term_clean)

tbl_example <- huxreg(mod.test.fe, mod.test.re, mod.test.re.fancy, 
                      coefs = c(coefs_named, Constant = "(Intercept)"),
                      stars = NULL, statistics = c(N = "nobs"), note = "") %>% 
  insert_row(c("Country effects", "Fixed", "Random", "Random"),
             after = nrow(.) - 2, copy_cell_props = FALSE) %>% 
  # Highlight identical cells
  set_bold(2:5, 2, TRUE) %>% 
  set_bold(c(8, 9, 12, 13), 4, TRUE)

tbl_example %>% print_hux()

	(1)	(2)	(3)
Total legal barriers	-0.091	-0.056
	(0.089)	(0.085)
Polity IV (0–10)	0.267	0.226
	(0.045)	(0.043)
Total legal barriers_between			-0.132
			(0.323)
Total legal barriers_within			-0.091
			(0.089)
Polity IV (0–10)_between			-0.165
			(0.155)
Polity IV (0–10)_within			0.267
			(0.045)
Constant	17.911	16.739	18.826
	(1.147)	(0.446)	(1.213)
Country effects	Fixed	Random	Random
N	4416	4416	4416

tbl_example %>% 
  to_md(max_width = 100) %>% 
  cat(file = here("Output", "tbl-within-between-example.md"))

All of the models we run use imputed data (\(m = 5\)) with crossed year and country random effects. Most explanatory and control variables are included in their meaned and demeaned forms, except for any indicator variables (since you can’t really average binary data). Additionally, we include the regular form of the current year’s ODA to account for temporal autocorrelation in aid. We do not split current ODA into within and between versions so that mathematically it can be subtracted out of the next year’s ODA in the dependent variable. Other mixed models functions like nlme::lme() allow you to define autoregressive correlation structures, but lme4::lmer() doesn’t, so we account for time with this differenced approach instead. It’s not perfect, but it works:

mod.test.no.oda <- lmer(total.oda_log_next_year ~ 
                          barriers.total_between + barriers.total_within +
                          polity_between + polity_within + 
                          gdp.capita_log_between + gdp.capita_log_within +
                          (1 | cowcode) + (1 | year),
                        data = filter(df.country.aid.demean.next_year.impute,
                                      m == "imp1"))

mod.test.oda.split <- lmer(total.oda_log_next_year ~ 
                             barriers.total_between + barriers.total_within +
                             polity_between + polity_within + 
                             total.oda_log_between + total.oda_log_within +
                             gdp.capita_log_between + gdp.capita_log_within +
                             (1 | cowcode) + (1 | year),
                           data = filter(df.country.aid.demean.next_year.impute,
                                         m == "imp1"))

mod.test.oda.nosplit <- lmer(total.oda_log_next_year ~ 
                               barriers.total_between + barriers.total_within +
                               polity_between + polity_within + 
                               total.oda_log +
                               gdp.capita_log_between + gdp.capita_log_within +
                               (1 | cowcode) + (1 | year),
                             data = filter(df.country.aid.demean.next_year.impute,
                                           m == "imp1"))

resid.no.oda <- acf(residuals(mod.test.no.oda), plot = FALSE)
resid.oda <- acf(residuals(mod.test.oda.nosplit), plot = FALSE)

ci.line <- qnorm((1 + 0.95) / 2) / sqrt(resid.no.oda$n.used)

acf.plot.data <- bind_rows(
  data_frame(Lag = resid.no.oda$lag[,,1], ACF = resid.no.oda$acf[,,1], 
             model = "No ODA"),
  data_frame(Lag = resid.oda$lag[,,1], ACF = resid.oda$acf[,,1], 
             model = "Current year’s ODA")
)

ggplot(acf.plot.data, aes(x = Lag, y = ACF, fill = model)) +
  geom_bar(stat = "identity", position = position_dodge(width = 1), width = 0.5) +
  geom_hline(yintercept = 0, size = 1) +
  geom_hline(yintercept = c(ci.line, -ci.line), size = 0.5, linetype = "dashed") +
  guides(fill = guide_legend(title = NULL)) +
  theme_donors()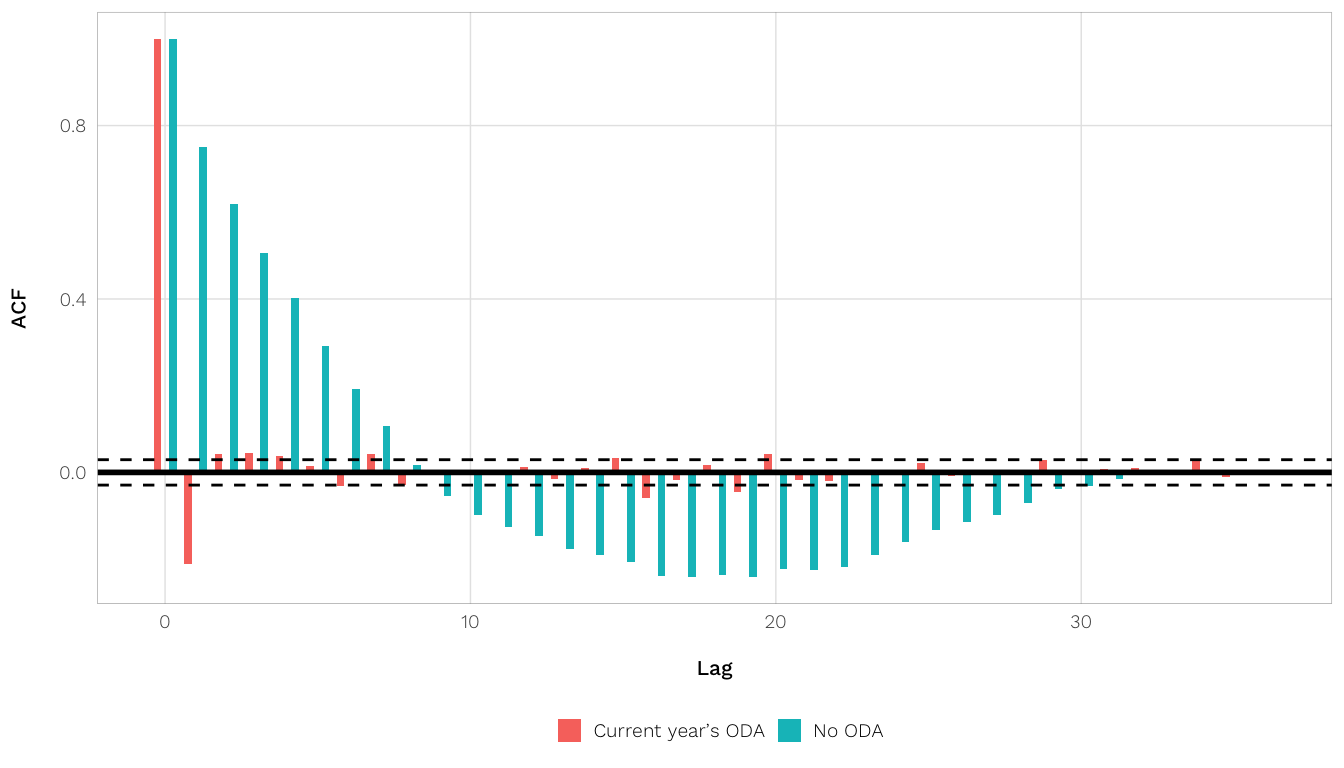

Not splitting current ODA into within and between also fixes another sticky mathematical issue. When the models are run with within and current ODA, the \(\sigma\) value for within-country variability becomes 0 for whatever reason (maybe it swallows up too much country level variability?). When \(\sigma = 0\), the between-group variability is too small to fully account for between effects, resulting in a “degenerate model” (see pages 10–11 here) and influencing the coefficients in weird ways. See below, where Model 1 uses the split current ODA and Model 2 doesn’t: \(\sigma\) in Model 2 exists and the coefficients are better estimated.

huxreg(mod.test.oda.split, mod.test.oda.nosplit,
       tidy_args = list(effects = "fixed"),
       statistics = c(N = "nobs"))

## Warning in FUN(X[[i]], ...): tidy() does not return p values for models of class data.frame; significance stars not
## printed.

## Warning in FUN(X[[i]], ...): tidy() does not return p values for models of class data.frame; significance stars not
## printed.

	(1)	(2)
(Intercept)	1.573	4.000
	(0.396)	(0.331)
barriers.total_between	-0.053	-0.044
	(0.037)	(0.037)
barriers.total_within	-0.032	-0.009
	(0.053)	(0.054)
polity_between	-0.008	0.003
	(0.019)	(0.019)
polity_within	-0.038	-0.036
	(0.027)	(0.027)
total.oda_log_between	0.972
	(0.010)
total.oda_log_within	0.823
	(0.009)
gdp.capita_log_between	-0.113	-0.236
	(0.036)	(0.035)
gdp.capita_log_within	-0.315	-0.203
	(0.147)	(0.148)
total.oda_log		0.885
		(0.007)
N	4480	4480
* p < 0.001; p < 0.01; * p < 0.05.

bind_rows(
  as.data.frame(VarCorr(mod.test.oda.split)) %>% mutate(model = "(1)"),
  as.data.frame(VarCorr(mod.test.oda.nosplit)) %>% mutate(model = "(2)")
) %>% 
  mutate(grp = ordered(fct_inorder(grp))) %>%
  select(`Random variable` = grp, sdcor, model) %>%
  spread(model, sdcor) %>% pandoc.table()

Random variable	(1)	(2)
cowcode	0	0
year	0.4206	0.3629
Residual	2.661	2.699

Results

The results of all models can be found in the “Bayesian models” notebook, since it takes so many hours to run them all.

Summary of hypotheses

findings.summary <- read_csv(here("Data", "data_manual", "findings_summary.csv"))

caption <- "Summary of findings {#tbl:findings-summary}"
findings.summary.table <- pandoc.table.return(findings.summary, justify = "lll",
                                              keep.line.breaks = TRUE, style = "grid",
                                              caption = caption)

cat(findings.summary.table)

Summary of findings {#tbl:findings-summary}
	Proposition	Finding
	If countries adopt restrictive NGO legislation…
H₁	…donors will reduce foreign aid	OECD donors reduce aid following additional barriers to advocacy
H₂	…donors will increase aid for tamer causes and reduce aid for politically sensitive causes	OECD donors increase funding for tamer causes following additional barriers to advocacy OECD donors increase funding for contentious causes as the overall civil society regulatory environment improves OECD donors increase funding for contentious causes following additional barriers to entry and funding
H₃	…donors will channel more aid through domestic NGOs and channel less aid through foreign NGOs	USAID channels more aid through domestic NGOs following additional barriers to funding USAID channels less aid through foreign NGOs following additional barriers to funding

cat(findings.summary.table, file = here("Output", "tbl-findings-summary.md"))

Robustness checks

Imputation

As discussed over in the data cleaning file, we impute data for the few variables that are missing. To show what difference imputation makes, the table below shows three pairs of models from H₁. The first two models are run on non-imputed data (so missing observations are deleted listwise), the second two models are run on 5 sets of imputed data, and the last two models are run on 10 sets of imputed data.

It’s clear that imputation makes a substantial difference—note the big differences between coefficients. However, the number of imputed datasets doesn’t seem to matter, since there are only trivial differences in coefficients when there are 5 and 10 datasets.

mods.robust.check.m.next_year.raw <- df.country.aid.demean.next_year.all %>%
  nest(-m) %>%
  mutate(mod.h1.barriers.total = data %>% 
           future_map(mod.h1.barriers.total,
                      "total.oda_log_next_year"),
         mod.h1.type.total = data %>% 
           future_map(mod.h1.type.total,
                      "total.oda_log_next_year"))

# Get model details and parameters
mods.robust.check.m.next_year <- mods.robust.check.m.next_year.raw %>%
  gather(model.name, model, -m, -data) %>%
  mutate(glance = model %>% map(broom::glance),
         tidy = model %>% map(broom::tidy, conf.int = TRUE))

# Meld the imputed models
mods.robust.check.m.next_year.melded.original <- mods.robust.check.m.next_year %>%
  filter(m == "original") %>%
  group_by(model.name) %>%
  nest() %>%
  mutate(tidy.melded = data %>% map(meld.imputed.models))

mods.robust.check.m.next_year.melded.m5 <- mods.robust.check.m.next_year %>%
  filter(m %in% paste0("imp", 1:5)) %>%
  group_by(model.name) %>%
  nest() %>%
  mutate(tidy.melded = data %>% map(meld.imputed.models))

mods.robust.check.m.next_year.melded.m10 <- mods.robust.check.m.next_year %>%
  filter(m != "original") %>%
  group_by(model.name) %>%
  nest() %>%
  mutate(tidy.melded = data %>% map(meld.imputed.models))

mods.robust.check.m.next_year.melded.all <- bind_rows(
  mods.robust.check.m.next_year.melded.original,
  mods.robust.check.m.next_year.melded.m5,
  mods.robust.check.m.next_year.melded.m10
) %>%
  mutate(imputations = data %>% map_dbl(~ nrow(.)),
         model.name = paste(model.name, imputations, sep = "_"))

stargazer.fake(mods.robust.check.m.next_year.melded.all) %>% cat()

	(1)	(2)	(3)	(4)	(5)	(6)
Fixed part
Total legal barriers_within	0.009 (0.051)		-0.054 (0.054)		-0.055 (0.054)
Total legal barriers_between	-0.004 (0.049)		-0.051 (0.038)		-0.051 (0.038)
Barriers to advocacy_within		-0.141 (0.233)		-0.424* (0.242)		-0.424* (0.242)
Barriers to advocacy_between		-0.067 (0.204)		-0.096 (0.157)		-0.096 (0.157)
Barriers to entry_within		0.224** (0.114)		0.104 (0.122)		0.103 (0.122)
Barriers to entry_between		0.004 (0.091)		0.116 (0.071)		0.116 (0.071)
Barriers to funding_within		-0.120 (0.131)		-0.032 (0.140)		-0.033 (0.139)
Barriers to funding_between		0.010 (0.101)		-0.166** (0.070)		-0.166** (0.070)
Polity IV (0–10)_within	0.054** (0.027)	0.050* (0.027)	-0.057** (0.028)	-0.061** (0.028)	-0.060** (0.028)	-0.064** (0.028)
Polity IV (0–10)_between	0.045* (0.026)	0.045* (0.026)	0.010 (0.020)	0.006 (0.021)	0.010 (0.020)	0.005 (0.021)
GDP per capita (log)_within	-0.288* (0.160)	-0.277* (0.160)	-0.397** (0.180)	-0.405** (0.181)	-0.402** (0.165)	-0.407** (0.164)
GDP per capita (log)_between	-0.275*** (0.050)	-0.274*** (0.051)	-0.177*** (0.040)	-0.173*** (0.040)	-0.177*** (0.040)	-0.173*** (0.040)
Trade as % of GDP_within	-0.004* (0.002)	-0.003* (0.002)	-0.004* (0.002)	-0.004 (0.002)	-0.004* (0.002)	-0.004* (0.002)
Trade as % of GDP_between	-0.002 (0.001)	-0.002 (0.001)	-0.002 (0.001)	-0.002 (0.001)	-0.002 (0.001)	-0.002 (0.001)
Corruption_within	0.139*** (0.044)	0.142*** (0.044)	0.052 (0.045)	0.053 (0.045)	0.051 (0.048)	0.052 (0.048)
Corruption_between	0.120*** (0.028)	0.120*** (0.029)	0.049** (0.023)	0.047** (0.023)	0.049** (0.023)	0.047** (0.023)
Total aid in present year (log)	0.750*** (0.010)	0.750*** (0.010)	0.872*** (0.007)	0.868*** (0.007)	0.872*** (0.007)	0.868*** (0.007)
Internal conflict in last 5 years	-0.049 (0.104)	-0.052 (0.105)	0.074 (0.102)	0.065 (0.103)	0.073 (0.102)	0.064 (0.102)
Natural disasters	0.048*** (0.016)	0.046*** (0.016)	0.035** (0.014)	0.034** (0.014)	0.035** (0.014)	0.034** (0.014)
After 1989	-0.054 (0.177)	-0.062 (0.176)	0.557*** (0.151)	0.583*** (0.150)	0.565*** (0.151)	0.591*** (0.150)
Constant	6.092*** (0.576)	6.105*** (0.585)	3.104*** (0.450)	2.999*** (0.452)	3.104*** (0.451)	2.999*** (0.452)
Random part
Within-country variability (\(\sigma\))	0.401 (NA)	0.407 (NA)	0.000 (0.000)	0.000 (0.000)	0.000 (0.000)	0.000 (0.000)
Within-year variability (\(\sigma\))	0.346 (NA)	0.342 (NA)	0.260 (0.006)	0.254 (0.006)	0.258 (0.004)	0.253 (0.004)
Residual random error (\(\sigma\))	2.422 (NA)	2.422 (NA)	2.693 (0.001)	2.691 (0.001)	2.693 (0.001)	2.691 (0.001)
Model details
Observations	4,067	4,067	4,480	4,480	4,480	4,480
Log likelihood (mean)	-9462.17	-9462.5	-10843.41	-10840.76	-10842.91	-10840.29
Imputed datasets (m)	0	0	5	5	10	10

Neutral regulations

mods.robust.neutral.regs.raw <- df.country.aid.demean.next_year.all %>%
  nest(-m) %>%
  mutate(mod.h1.neutral.reg = data %>% 
           future_map(mod.h1.neutral.reg,
                      "total.oda_log_next_year"),
         mod.h1.neutral.fund = data %>% 
           future_map(mod.h1.neutral.fund,
                      "total.oda_log_next_year"),
         mod.h2.neutral.reg = data %>% 
           future_map(mod.h2.neutral.reg,
                      "prop.contentious_logit_next_year"),
         mod.h2.neutral.fund = data %>% 
           future_map(mod.h2.neutral.fund,
                      "prop.contentious_logit_next_year"))

mods.robust.neutral.regs.raw.h3 <- df.country.aid.us.demean.next_year.both %>%
  nest(-m) %>%
  mutate(mod.h3.dom.neutral.reg = data %>% 
           future_map(mod.h3.dom.neutral.reg,
                      "prop.ngo.dom_logit_next_year"),
         mod.h3.dom.neutral.fund = data %>% 
           future_map(mod.h3.dom.neutral.fund,
                      "prop.ngo.dom_logit_next_year"),
         mod.h3.for.neutral.reg = data %>% 
           future_map(mod.h3.for.neutral.reg,
                      "prop.ngo.foreign_logit_next_year"),
         mod.h3.for.neutral.fund = data %>% 
           future_map(mod.h3.for.neutral.fund,
                      "prop.ngo.foreign_logit_next_year"))

# Get model details and parameters
mods.robust.neutral.regs <- mods.robust.neutral.regs.raw %>%
  gather(model.name, model, -m, -data) %>%
  mutate(glance = model %>% map(broom::glance),
         tidy = model %>% map(broom::tidy, conf.int = TRUE))

mods.robust.neutral.regs.h3 <- mods.robust.neutral.regs.raw.h3 %>%
  gather(model.name, model, -m, -data) %>%
  mutate(glance = model %>% map(broom::glance),
         tidy = model %>% map(broom::tidy, conf.int = TRUE))

# Meld the imputed models
mods.robust.neutral.regs.melded.h1 <- mods.robust.neutral.regs %>%
  filter(m != "original", str_detect(model.name, "h1")) %>%
  group_by(model.name) %>%
  nest() %>%
  mutate(tidy.melded = data %>% map(meld.imputed.models))

mods.robust.neutral.regs.melded.h2 <- mods.robust.neutral.regs %>%
  filter(m != "original", str_detect(model.name, "h2")) %>%
  group_by(model.name) %>%
  nest() %>%
  mutate(tidy.melded = data %>% map(~ meld.imputed.models(., exponentiate = TRUE)))

mods.robust.neutral.regs.melded.h3 <- mods.robust.neutral.regs.h3 %>%
  filter(m != "original") %>%
  group_by(model.name) %>%
  nest() %>%
  mutate(tidy.melded = data %>% map(~ meld.imputed.models(., exponentiate = TRUE)))

Neutral regulations and overall aid (H1)

table.robust.neutral.regs.h1 <- mods.robust.neutral.regs.melded.h1 %>%
  stargazer.fake(exponentiate = FALSE) %>%
  cat()

	(1)	(2)
Fixed part
Registration requirement	-0.103 (0.091)
Funding disclosure requirement		-0.088 (0.092)
GDP per capita (log)_within	-0.409** (0.164)	-0.411** (0.164)
GDP per capita (log)_between	-0.165*** (0.040)	-0.169*** (0.039)
Trade as % of GDP_within	-0.004* (0.002)	-0.004* (0.002)
Trade as % of GDP_between	-0.002 (0.001)	-0.002* (0.001)
Corruption_within	0.055 (0.049)	0.054 (0.049)
Corruption_between	0.041* (0.021)	0.040* (0.021)
Total aid in present year (log)	0.874*** (0.007)	0.873*** (0.007)
Internal conflict in last 5 years	0.090 (0.101)	0.095 (0.101)
Natural disasters	0.031** (0.014)	0.032** (0.014)
After 1989	0.474*** (0.148)	0.468*** (0.148)
Constant	3.075*** (0.430)	3.135*** (0.426)
Random part
Within-country variability (\(\sigma\))	0.000 (0.000)	0.000 (0.000)
Within-year variability (\(\sigma\))	0.273 (0.005)	0.274 (0.005)
Residual random error (\(\sigma\))	2.694 (0.001)	2.694 (0.001)
Model details
Observations	4,480	4,480
Log likelihood (mean)	-10837.94	-10838.11
Imputed datasets (m)	10	10

Neutral regulations and tamer causes (H2)

table.robust.neutral.regs.h2 <- mods.robust.neutral.regs.melded.h2 %>%
  filter(str_detect(model.name, "h2")) %>%
  stargazer.fake(exponentiate = TRUE) %>%
  cat()

	(1)	(2)
Fixed part (odds ratios)
Registration requirement	1.009 (0.072)
Funding disclosure requirement		0.908 (0.066)
Polity IV (0–10)_within	1.029* (0.016)	1.029* (0.016)
Polity IV (0–10)_between	1.092*** (0.023)	1.091*** (0.022)
GDP per capita (log)_within	0.973 (0.089)	0.976 (0.089)
GDP per capita (log)_between	0.699*** (0.032)	0.701*** (0.032)
Trade as % of GDP_within	0.998* (0.001)	0.998* (0.001)
Trade as % of GDP_between	1.002* (0.001)	1.002* (0.001)
Corruption_within	1.054** (0.027)	1.057** (0.027)
Corruption_between	1.067** (0.028)	1.066** (0.027)
Proportion of contentious aid in present year (logit)	1.280*** (0.019)	1.281*** (0.019)
Internal conflict in last 5 years	1.065 (0.068)	1.065 (0.068)
Natural disasters	0.991 (0.010)	0.991 (0.010)
After 1989	4.799*** (1.010)	4.884*** (1.042)
Constant	0.091*** (0.044)	0.092*** (0.044)
Random part (original coefficients)
Within-country variability (\(\sigma\))	0.491 (0.002)	0.481 (0.001)
Within-year variability (\(\sigma\))	0.504 (0.002)	0.512 (0.002)
Residual random error (\(\sigma\))	1.327 (0.000)	1.327 (0.000)
Model details
Observations	3,922	3,922
Log likelihood (mean)	-6862.09	-6861.22
Imputed datasets (m)	10	10

Neutral regulations and NGOs (H3)

table.robust.neutral.regs.h3 <- mods.robust.neutral.regs.melded.h3 %>%
  stargazer.fake(exponentiate = TRUE) %>%
  cat()

	(1)	(2)	(3)	(4)
Fixed part (odds ratios)
Registration requirement	1.178 (0.149)		0.724** (0.103)
Funding disclosure requirement		1.071 (0.129)		1.005 (0.137)
Polity IV (0–10)_within	0.879** (0.049)	0.878** (0.049)	1.047 (0.063)	1.045 (0.063)
Polity IV (0–10)_between	0.999 (0.029)	0.994 (0.028)	0.964 (0.032)	0.977 (0.032)
GDP per capita (log)_within	2.009*** (0.525)	2.004*** (0.529)	0.302*** (0.077)	0.280*** (0.072)
GDP per capita (log)_between	1.037 (0.074)	1.048 (0.074)	0.726*** (0.060)	0.707*** (0.059)
Trade as % of GDP_within	1.000 (0.003)	1.000 (0.003)	0.997 (0.003)	0.997 (0.003)
Trade as % of GDP_between	0.995*** (0.002)	0.995*** (0.002)	1.000 (0.002)	0.999 (0.002)
Corruption_within	1.200** (0.091)	1.200** (0.091)	1.140 (0.095)	1.133 (0.094)
Corruption_between	1.142*** (0.045)	1.142*** (0.045)	1.290*** (0.059)	1.292*** (0.059)
Proportion of aid to domestic NGOs in present year (logit)	1.389*** (0.031)	1.391*** (0.031)
Proportion of aid to foreign NGOs in present year (logit)			1.386*** (0.028)	1.386*** (0.028)
Internal conflict in last 5 years	1.228 (0.165)	1.215 (0.163)	1.151 (0.173)	1.183 (0.178)
Natural disasters	0.991 (0.015)	0.990 (0.015)	1.035** (0.018)	1.035** (0.018)
Constant	0.022*** (0.017)	0.022*** (0.017)	0.712 (0.624)	0.685 (0.605)
Random part (original coefficients)
Within-country variability (\(\sigma\))	0.711 (0.002)	0.712 (0.002)	0.844 (0.001)	0.850 (0.001)
Within-year variability (\(\sigma\))	0.169 (0.002)	0.173 (0.002)	0.093 (0.006)	0.090 (0.004)
Residual random error (\(\sigma\))	1.551 (0.001)	1.552 (0.001)	1.700 (0.002)	1.702 (0.002)
Model details
Observations	1,751	1,751	1,751	1,751
Log likelihood (mean)	-3374.09	-3374.81	-3537.15	-3539.75
Imputed datasets (m)	5	5	5	5

Longer lags: H₁

Looking at aid 2 years and 5 years after the change in anti-NGO legislation shows similar trends to 1 year after.

mods.h1.after_2.raw <- df.country.aid.demean.after_2.impute %>%
  nest(-m) %>%
  mutate(mod.h1.barriers.total = data %>% 
           future_map(mod.h1.barriers.total, "total.oda_log_next_year"),
         mod.h1.type.total = data %>% 
           future_map(mod.h1.type.total, "total.oda_log_next_year"),
         mod.h1.csre = data %>% 
           future_map(mod.h1.csre, "total.oda_log_next_year"))

# Get model details and parameters
mods.h1.after_2 <- mods.h1.after_2.raw %>%
  gather(model.name, model, -m, -data) %>%
  mutate(glance = model %>% map(broom::glance),
         tidy = model %>% map(broom::tidy, conf.int = TRUE))

# Meld the imputed models
mods.h1.after_2.melded <- mods.h1.after_2 %>%
  filter(m != "original") %>%
  group_by(model.name) %>%
  nest() %>%
  mutate(tidy.melded = data %>% map(meld.imputed.models))

mods.h1.after_5.raw <- df.country.aid.demean.after_5.impute %>%
  nest(-m) %>%
  mutate(mod.h1.barriers.total = data %>% 
           future_map(mod.h1.barriers.total, "total.oda_log_next_year"),
         mod.h1.type.total = data %>% 
           future_map(mod.h1.type.total, "total.oda_log_next_year"),
         mod.h1.csre = data %>% 
           future_map(mod.h1.csre, "total.oda_log_next_year"))

# Get model details and parameters
mods.h1.after_5 <- mods.h1.after_5.raw %>%
  gather(model.name, model, -m, -data) %>%
  mutate(glance = model %>% map(broom::glance),
         tidy = model %>% map(broom::tidy, conf.int = TRUE))

# Meld the imputed models
mods.h1.after_5.melded <- mods.h1.after_5 %>%
  filter(m != "original") %>%
  group_by(model.name) %>%
  nest() %>%
  mutate(tidy.melded = data %>% map(meld.imputed.models))

Effect on ODA after 2 years

stargazer.fake(mods.h1.after_2.melded) %>% cat()

	(1)	(2)	(3)
Fixed part
Total legal barriers_within	-0.069 (0.057)
Total legal barriers_between	-0.052 (0.039)
Barriers to advocacy_within		-0.444* (0.257)
Barriers to advocacy_between		-0.088 (0.163)
Barriers to entry_within		0.070 (0.128)
Barriers to entry_between		0.128* (0.074)
Barriers to funding_within		-0.029 (0.148)
Barriers to funding_between		-0.180** (0.073)
Civil society reg. env. (CSRE)_within			-0.020 (0.043)
Civil society reg. env. (CSRE)_between			0.058 (0.037)
Polity IV (0–10)_within	-0.060** (0.029)	-0.063** (0.029)	-0.042 (0.040)
Polity IV (0–10)_between	0.009 (0.021)	0.004 (0.021)	-0.021 (0.033)
GDP per capita (log)_within	-0.461** (0.189)	-0.471** (0.189)	-0.470** (0.189)
GDP per capita (log)_between	-0.177*** (0.041)	-0.172*** (0.041)	-0.177*** (0.041)
Trade as % of GDP_within	-0.004 (0.002)	-0.003 (0.002)	-0.003 (0.002)
Trade as % of GDP_between	-0.002 (0.001)	-0.002 (0.001)	-0.002 (0.001)
Corruption_within	0.054 (0.047)	0.056 (0.047)	0.054 (0.047)
Corruption_between	0.046* (0.023)	0.044* (0.023)	0.049** (0.023)
Total aid in present year (log)	0.865*** (0.007)	0.861*** (0.007)	0.865*** (0.007)
Internal conflict in last 5 years	0.083 (0.105)	0.075 (0.106)	0.119 (0.105)
Natural disasters	0.037** (0.015)	0.036** (0.015)	0.035** (0.015)
After 1989	0.590*** (0.151)	0.618*** (0.150)	0.571*** (0.156)
Constant	3.225*** (0.458)	3.109*** (0.460)	3.204*** (0.457)
Random part
Within-country variability (\(\sigma\))	0.000 (0.000)	0.000 (0.000)	0.000 (0.000)
Within-year variability (\(\sigma\))	0.252 (0.007)	0.246 (0.007)	0.265 (0.007)
Residual random error (\(\sigma\))	2.730 (0.001)	2.727 (0.001)	2.729 (0.001)
Model details
Observations	4,340	4,340	4,340
Log likelihood (mean)	-10562.13	-10559.29	-10562.71
Imputed datasets (m)	5	5	5

Effect on ODA after 5 years

stargazer.fake(mods.h1.after_5.melded) %>% cat()

	(1)	(2)	(3)
Fixed part
Total legal barriers_within	-0.113* (0.064)
Total legal barriers_between	-0.055 (0.039)
Barriers to advocacy_within		-0.313 (0.291)
Barriers to advocacy_between		-0.025 (0.169)
Barriers to entry_within		-0.047 (0.138)
Barriers to entry_between		0.139* (0.076)
Barriers to funding_within		-0.091 (0.166)
Barriers to funding_between		-0.213*** (0.075)
Civil society reg. env. (CSRE)_within			-0.031 (0.044)
Civil society reg. env. (CSRE)_between			0.040 (0.036)
Polity IV (0–10)_within	-0.054* (0.029)	-0.056* (0.029)	-0.029 (0.041)
Polity IV (0–10)_between	0.005 (0.020)	0.002 (0.021)	-0.011 (0.032)
GDP per capita (log)_within	-0.477** (0.191)	-0.487** (0.191)	-0.502*** (0.190)
GDP per capita (log)_between	-0.116*** (0.041)	-0.111*** (0.041)	-0.118*** (0.041)
Trade as % of GDP_within	-0.002 (0.002)	-0.002 (0.002)	-0.002 (0.002)
Trade as % of GDP_between	-0.003** (0.001)	-0.003** (0.001)	-0.002** (0.001)
Corruption_within	0.025 (0.048)	0.027 (0.048)	0.026 (0.048)
Corruption_between	0.028 (0.023)	0.028 (0.023)	0.031 (0.023)
Total aid in present year (log)	0.861*** (0.007)	0.856*** (0.008)	0.861*** (0.007)
Internal conflict in last 5 years	0.099 (0.105)	0.099 (0.106)	0.131 (0.106)
Natural disasters	0.029* (0.015)	0.027* (0.015)	0.026* (0.015)
After 1989	0.727*** (0.116)	0.752*** (0.115)	0.707*** (0.122)
Constant	3.025*** (0.446)	2.884*** (0.448)	2.965*** (0.447)
Random part
Within-country variability (\(\sigma\))	0.000 (0.000)	0.000 (0.000)	0.000 (0.000)
Within-year variability (\(\sigma\))	0.100 (0.004)	0.090 (0.005)	0.112 (0.003)
Residual random error (\(\sigma\))	2.628 (0.001)	2.626 (0.001)	2.629 (0.001)
Model details
Observations	3,920	3,920	3,920
Log likelihood (mean)	-9386.61	-9384	-9388.68
Imputed datasets (m)	5	5	5

Longer lags: H₂

mods.h2.after_2.raw <- df.country.aid.demean.after_2.impute %>%
  nest(-m) %>%
  mutate(mod.h2.barriers.total = data %>% 
           future_map(mod.h2.barriers.total, "prop.contentious_logit_next_year"),
         mod.h2.type.total = data %>% 
           future_map(mod.h2.type.total, "prop.contentious_logit_next_year"),
         mod.h2.csre = data %>% 
           future_map(mod.h2.csre, "prop.contentious_logit_next_year"))

# Get model details and parameters
mods.h2.after_2 <- mods.h2.after_2.raw %>%
  gather(model.name, model, -m, -data) %>%
  mutate(glance = model %>% map(broom::glance),
         tidy = model %>% map(broom::tidy, conf.int = TRUE))

# Meld the imputed models
mods.h2.after_2.melded <- mods.h2.after_2 %>%
  filter(m != "original") %>%
  group_by(model.name) %>%
  nest() %>%
  mutate(tidy.melded = data %>% map(meld.imputed.models))

mods.h2.after_5.raw <- df.country.aid.demean.after_5.impute %>%
  nest(-m) %>%
  mutate(mod.h2.barriers.total = data %>% 
           future_map(mod.h2.barriers.total, "prop.contentious_logit_next_year"),
         mod.h2.type.total = data %>% 
           future_map(mod.h2.type.total, "prop.contentious_logit_next_year"),
         mod.h2.csre = data %>% 
           future_map(mod.h2.csre, "prop.contentious_logit_next_year"))

# Get model details and parameters
mods.h2.after_5 <- mods.h2.after_5.raw %>%
  gather(model.name, model, -m, -data) %>%
  mutate(glance = model %>% map(broom::glance),
         tidy = model %>% map(broom::tidy, conf.int = TRUE))

# Meld the imputed models
mods.h2.after_5.melded <- mods.h2.after_5 %>%
  filter(m != "original") %>%
  group_by(model.name) %>%
  nest() %>%
  mutate(tidy.melded = data %>% map(meld.imputed.models))

Effect on contentious aid after 2 years

stargazer.fake(mods.h2.after_2.melded) %>% cat()

	(1)	(2)	(3)
Fixed part
Total legal barriers_within	0.041 (0.031)
Total legal barriers_between	-0.017 (0.046)
Barriers to advocacy_within		-0.255* (0.133)
Barriers to advocacy_between		-0.076 (0.184)
Barriers to entry_within		0.099 (0.067)
Barriers to entry_between		0.086 (0.085)
Barriers to funding_within		0.124 (0.075)
Barriers to funding_between		-0.098 (0.094)
Civil society reg. env. (CSRE)_within			0.077*** (0.024)
Civil society reg. env. (CSRE)_between			0.046 (0.043)
Polity IV (0–10)_within	0.031* (0.016)	0.030* (0.016)	-0.016 (0.022)
Polity IV (0–10)_between	0.085*** (0.024)	0.082*** (0.024)	0.056 (0.038)
GDP per capita (log)_within	-0.026 (0.095)	-0.031 (0.096)	-0.004 (0.095)
GDP per capita (log)_between	-0.360*** (0.047)	-0.356*** (0.047)	-0.360*** (0.047)
Trade as % of GDP_within	-0.002 (0.001)	-0.002 (0.001)	-0.002* (0.001)
Trade as % of GDP_between	0.002 (0.001)	0.002 (0.001)	0.002* (0.001)
Corruption_within	0.055** (0.027)	0.056** (0.027)	0.061** (0.027)
Corruption_between	0.063** (0.027)	0.062** (0.027)	0.067** (0.027)
Proportion of contentious aid in present year (logit)	0.244*** (0.015)	0.241*** (0.015)	0.239*** (0.015)
Internal conflict in last 5 years	0.057 (0.066)	0.048 (0.066)	0.079 (0.066)
Natural disasters	-0.008 (0.011)	-0.008 (0.011)	-0.010 (0.011)
After 1989	1.520*** (0.209)	1.533*** (0.210)	1.456*** (0.210)
Constant	-2.315*** (0.502)	-2.443*** (0.512)	-2.245*** (0.495)
Random part
Within-country variability (\(\sigma\))	0.497 (0.002)	0.500 (0.002)	0.498 (0.002)
Within-year variability (\(\sigma\))	0.493 (0.002)	0.496 (0.002)	0.495 (0.002)
Residual random error (\(\sigma\))	1.336 (0.000)	1.335 (0.000)	1.334 (0.000)
Model details
Observations	3,808	3,808	3,808
Log likelihood (mean)	-6693.91	-6694.1	-6689.21
Imputed datasets (m)	5	5	5

Effect on contentious aid after 5 years

stargazer.fake(mods.h2.after_5.melded) %>% cat()

	(1)	(2)	(3)
Fixed part
Total legal barriers_within	0.026 (0.036)
Total legal barriers_between	-0.012 (0.046)
Barriers to advocacy_within		-0.330** (0.156)
Barriers to advocacy_between		-0.025 (0.192)
Barriers to entry_within		0.106 (0.076)
Barriers to entry_between		0.075 (0.088)
Barriers to funding_within		0.116 (0.089)
Barriers to funding_between		-0.093 (0.097)
Civil society reg. env. (CSRE)_within			0.080*** (0.025)
Civil society reg. env. (CSRE)_between			0.036 (0.043)
Polity IV (0–10)_within	0.028 (0.017)	0.026 (0.017)	-0.020 (0.023)
Polity IV (0–10)_between	0.088*** (0.024)	0.087*** (0.024)	0.065* (0.037)
GDP per capita (log)_within	-0.062 (0.107)	-0.067 (0.107)	-0.046 (0.106)
GDP per capita (log)_between	-0.370*** (0.047)	-0.367*** (0.048)	-0.371*** (0.047)
Trade as % of GDP_within	-0.001 (0.001)	-0.001 (0.001)	-0.002 (0.001)
Trade as % of GDP_between	0.002 (0.001)	0.002 (0.001)	0.002* (0.001)
Corruption_within	0.072** (0.030)	0.073** (0.029)	0.077*** (0.029)
Corruption_between	0.058** (0.027)	0.058** (0.027)	0.061** (0.027)
Proportion of contentious aid in present year (logit)	0.232*** (0.016)	0.229*** (0.016)	0.227*** (0.016)
Internal conflict in last 5 years	0.089 (0.070)	0.081 (0.070)	0.108 (0.070)
Natural disasters	-0.008 (0.012)	-0.008 (0.012)	-0.010 (0.012)
After 1989	1.443*** (0.205)	1.456*** (0.207)	1.365*** (0.205)
Constant	-2.324*** (0.494)	-2.442*** (0.507)	-2.253*** (0.490)
Random part
Within-country variability (\(\sigma\))	0.497 (0.002)	0.502 (0.002)	0.499 (0.002)
Within-year variability (\(\sigma\))	0.474 (0.002)	0.477 (0.002)	0.470 (0.001)
Residual random error (\(\sigma\))	1.360 (0.000)	1.359 (0.000)	1.358 (0.000)
Model details
Observations	3,446	3,446	3,446
Log likelihood (mean)	-6122.67	-6122.58	-6117.85
Imputed datasets (m)	5	5	5

LS0tCnRpdGxlOiAiTW9kZWxzIgphdXRob3I6ICJTdXBhcm5hIENoYXVkaHJ5IGFuZCBBbmRyZXcgSGVpc3MiCmRhdGU6ICJgciBmb3JtYXQoU3lzLnRpbWUoKSwgJyVGJylgIgpvdXRwdXQ6IAogIGh0bWxfZG9jdW1lbnQ6CiAgICBjb2RlX2ZvbGRpbmc6IGhpZGUKZWRpdG9yX29wdGlvbnM6IAogIGNodW5rX291dHB1dF90eXBlOiBjb25zb2xlCi0tLQoKYGBge3IgZWNobz1GQUxTRSwgd2FybmluZz1GQUxTRSwgbWVzc2FnZT1GQUxTRX0KIyBFeHRlcm5hbGl6ZSB0aGVzZSBjaHVua3M6CiMgaHR0cDovL3pldnJvc3MuY29tL2Jsb2cvMjAxNC8wNy8wOS9tYWtpbmctdXNlLW9mLWV4dGVybmFsLXItY29kZS1pbi1rbml0ci1hbmQtci1tYXJrZG93bi8KIyBFeGNlcHQgQGtuaXRyIHdhcyByZXBsYWNlZCB3aXRoIGZvdXIgZGFzaGVzIGJlY2F1c2Ugb2YgUlN0dWRpbyBzZWN0aW9uIGZvbGRpbmcKaWYgKGlzVFJVRShnZXRPcHRpb24oJ2tuaXRyLmluLnByb2dyZXNzJykpKSB7CiAga25pdHI6OnJlYWRfY2h1bmsoaGVyZTo6aGVyZSgibGliIiwgIm1vZGVscy1jaHVua3MuUiIpKQp9IGVsc2UgewogIHNvdXJjZShoZXJlOjpoZXJlKCJsaWIiLCAibW9kZWxzLWNodW5rcy5SIikpCn0KYGBgCgpgYGB7ciBsb2FkLWxpYnJhcmllcywgbWVzc2FnZT1GQUxTRX0KYGBgCgpgYGB7ciBsb2FkLWRhdGEsIGNhY2hlPVRSVUUsIG1lc3NhZ2U9RkFMU0V9CmBgYAoKYGBge3IgZnVycnIsIG1lc3NhZ2U9RkFMU0V9CmxpYnJhcnkoZnVycnIpCnBsYW4obXVsdGlwcm9jZXNzKQpgYGAKCmBgYHtyIGh1eHRhYmxlLWZ1bmN0aW9uc30KIyBQcmludCBjb3JyZWN0IGh1eHRhYmxlIHRhYmxlIGRlcGVuZGluZyBvbiB0aGUgdHlwZSBvZiBvdXRwdXQuCiMKIyBUZWNobmljYWxseSB0aGlzIGlzbid0IGNvbXBsZXRlbHkgbmVjZXNzYXJ5LCBzaW5jZSBodXh0YWJsZSBjYW4gb3V0cHV0IGEKIyBtYXJrZG93biB0YWJsZSwgd2hpY2ggaXMgb3N0ZW5zaWJseSB1bml2ZXJzYWwgZm9yIGFsbCBvdXRwdXQgdHlwZXMuIEhvd2V2ZXIsCiMgbWFya2Rvd24gdGFibGVzIGFyZSBpbmhlcmVudGx5IGxpbWl0ZWQgaW4gaG93IGZhbmN5IHRoZXkgY2FuIGJlIChlLmcuIHRoZXkKIyBkb24ndCBzdXBwb3J0IGNvbHVtbiBzcGFucyksIHNvIEkgaW5zdGVhZCBsZXQgdGhlIHJlZ3Jlc3Npb24gdGFibGUgdXNlCiMgaHV4dGFibGUncyBmYW5jeSBmb3JtYXR0aW5nIGZvciBodG1sIGFuZCBQREYgYW5kIG1hcmtkb3duIGV2ZXJ5d2hlcmUgZWxzZS4KaWYgKGlzVFJVRShnZXRPcHRpb24oJ2tuaXRyLmluLnByb2dyZXNzJykpKSB7CiAgZmlsZV9mb3JtYXQgPC0gcm1hcmtkb3duOjphbGxfb3V0cHV0X2Zvcm1hdHMoa25pdHI6OmN1cnJlbnRfaW5wdXQoKSkKfSBlbHNlIHsKICBmaWxlX2Zvcm1hdCA8LSAiIgp9CgpwcmludF9odXggPC0gZnVuY3Rpb24oeCkgewogIGlmICgiaHRtbF9kb2N1bWVudCIgJWluJSBmaWxlX2Zvcm1hdCkgewogICAgcHJpbnRfaHRtbCh4KQogIH0gZWxzZSBpZiAoInBkZl9kb2N1bWVudCIgJWluJSBmaWxlX2Zvcm1hdCkgewogICAgcHJpbnRfbGF0ZXgoeCkKICB9IGVsc2UgaWYgKCJ3b3JkX2RvY3VtZW50IiAlaW4lIGZpbGVfZm9ybWF0KSB7CiAgICBwcmludF9tZCh4KQogIH0gZWxzZSB7CiAgICBwcmludCh4KQogIH0KfQpgYGAKCmBgYHtyIGhlbHBmdWwtZnVuY3Rpb25zfQpgYGAKCiMjIERlcGVuZGVudCB2YXJpYWJsZXMKCkFzIGV4cGxhaW5lZCBpbiBlYWNoIHNlY3Rpb24gYmVsb3csIHdlIGhhdmUgdG8gdHJhbnNmb3JtIGFuZCBvcGVyYXRpb25hbGl6ZSB0aGUgZGVwZW5kZW50IHZhcmlhYmxlIChmb3JlaWduIGFpZCkgaW4gZGlmZmVyZW50IHdheXMgZm9yIGVhY2ggaHlwb3RoZXNpcy4gVGhlIHRhYmxlIGJlbG93cyBzdW1tYXJpemVzIGVhY2ggc2ltcGxpZmllZCBtb2RlbCBzcGVjaWZpY2F0aW9uLgoKJCQKXGJlZ2lue2FsaWduZWR9Clxib2xkc3ltYm9se0hfMX0mOiBsbiggXHRleHR7T0RBfV97XHRleHR7T0VDRH19IClfe2ksIHQrMX0gJj0gXHRleHR7TkdPIGxlZ2lzbGF0aW9ufV97aXR9ICsgXHRleHR7Y29udHJvbHN9X3tpdH0gXFwKXGJvbGRzeW1ib2x7SF8yfSY6IGxuKCBcZnJhY3tcdGV4dHtjb250ZW50aW91cyBPREF9X3tcdGV4dHtPRUNEfX19e1x0ZXh0e25vbmNvbnRlbnRpb3VzIE9EQX1fe1x0ZXh0e09FQ0R9fX0gKV97aSwgdCsxfSAmPSBcdGV4dHtOR08gbGVnaXNsYXRpb259X3tpdH0gKyBcdGV4dHtjb250cm9sc31fe2l0fSBcXApcYm9sZHN5bWJvbHtIXzN9JjogbG4oIFxmcmFje1x0ZXh0e0FpZCB0byAoZG9tZXN0aWMgb3IgZm9yZWlnbikgTkdPc31fe1x0ZXh0e1VTQUlEfX19e1x0ZXh0e0FpZCB0byBvdGhlciBjaGFubmVsc31fe1x0ZXh0e1VTQUlEfX19IClfe2ksIHQrMX0gJj0gXHRleHR7TkdPIGxlZ2lzbGF0aW9ufV97aXR9ICsgXHRleHR7Y29udHJvbHN9X3tpdH0KXGVuZHthbGlnbmVkfQokJCB7I2VxOmFsbC1tb2RlbHMtZHZzfQoKIyMgR2VuZXJhbCBtb2RlbCBzcGVjaWZpY2F0aW9ucyBhbmQgY29udHJvbHMKCldlIHVzZSBhIHN0YW5kYXJkIHNldCBvZiBjb250cm9scyBpbiBlYWNoIG1vZGVsIChbZXhwbGFpbmVkIGluIG1vcmUgZGV0YWlsIGhlcmVdKDAxX2dldC1tZXJnZS1kYXRhLmh0bWwjb3RoZXJfY29udHJvbHNfYW5kX2FsdGVybmF0aXZlX2h5cG90aGVzZXMpKToKCi0gRGVtb2NyYWN5OiBgcG9saXR5YAotIFdlYWx0aDogYGdkcC5jYXBpdGFfbG9nYCAobG9nZ2VkIHNvIGl0J3Mgb24gdGhlIHNhbWUgc2NhbGUgYXMgdGhlIG90aGVyIHZhcmlhYmxlcykgCi0gR292ZXJubWVudCBjYXBhY2l0eTogYGNvcnJ1cHRpb25gCi0gQmFkIHN0dWZmOiBgaW50ZXJuYWwuY29uZmxpY3QucGFzdC41YCBhbmQgYG5hdHVyYWxfZGlzYXN0ZXIub2NjdXJyZW5jZWAKCkZvbGxvd2luZyBbQmVsbCBhbmQgSm9uZXMgKDIwMTUpXShodHRwOi8vZHguZG9pLm9yZy8xMC4xMDE3L3Bzcm0uMjAxNC43KSwgd2UgdXNlIGNyb3NzZWQgcmFuZG9tIGVmZmVjdHMgZm9yIGNvdW50cnkgYW5kIHllYXIgYW5kIHVzZSBhIGNvbWJpbmF0aW9uIG9mIG1lYW5lZCBhbmQgZGVtZWFuZWQgdmVyc2lvbnMgb2YgZWFjaCBjb250aW51b3VzIHZhcmlhYmxlIHRvIGVzdGltYXRlIGJvdGggdGhlIHdpdGhpbiBhbmQgYmV0d2VlbiBlZmZlY3RzIG9mIGVhY2ggdmFyaWFibGUuIAoKJCQgeV97aSwgdCArIDF9ID0gXGJldGFfMCArIFxiZXRhXzEgKHhfe2l0fSAtIFxiYXJ7eH1faSkgKyBcYmV0YV8yIFxiYXJ7eH1faSArIFxsZG90cyAkJAoKVGhpcyBhcHByb2FjaCBoYXMgbXVsdGlwbGUgYmVuZWZpdHMuIFRoZSBjb2VmZmljaWVudHMgZm9yIHRoZSBkZW1lYW5lZCB2YXJpYWJsZXMgYXJlIHJvdWdobHkgZXF1aXZhbGVudCB0byB0aGVpciBjb3JyZXNwb25kaW5nIGNvZWZmaWNpZW50cyBpbiBhIGZpeGVkIGVmZmVjdHMgbW9kZWwsIGJ1dCBhIGZpeGVkIGVmZmVjdHMgbW9kZWwgYXNzdW1lcyB0aGF0IHRoZSBiZXR3ZWVuIGVmZmVjdCAoY2FwdHVyZWQgYnkgdGhlIG1lYW4gdmFyaWFibGVzKSBpcyAwLCB3aGljaCBpcyBub3QgdGhlIGNhc2UuIEEgcmFuZG9tIGVmZmVjdHMgbW9kZWwgc3BlY2lmaWVkIGluIHRoaXMgbWFubmVyIGlzIG1vcmUgaW50ZXJwcmV0YWJsZSwgYXMgaXQgY2xlYXJseSBzZXBhcmF0ZXMgdGhlIHdpdGhpbiBhbmQgYmV0d2VlbiBlZmZlY3RzIChhZ2Fpbiwgd2l0aGluID0gZGVtZWFuZWQsIGJldHdlZW4gPSBtZWFuKS4KCkhlcmUncyBwcm9vZiBvZiBob3cgaXQgd29ya3MgaW4gc29tZSBzaW1wbGUgbW9kZWxzLiBNb2RlbCAxIGlzIGEgYmFzaWMgT0xTIHdpdGggY291bnRyeSBmaXhlZCBlZmZlY3RzLiBNb2RlbCAyIGlzIGEgYmFzaWMgT0xTIHdpdGggY291bnRyeSByYW5kb20gZWZmZWN0cywgYnV0IHBvdGVudGlhbGx5IG1pc3NwZWNpZmllZCwgc2luY2UgdGhlIGJldHdlZW4gYW5kIHdpdGhpbiBlZmZlY3RzIGFyZSBjb25mbGF0ZWQuIE1vZGVsIDMgaXMgYSBiYXNpYyBPTFMgd2l0aCBjb3VudHJ5IHJhbmRvbSBlZmZlY3RzIHNwZWNpZmllZCB3aXRoIGJldHdlZW4gKG1lYW47ICRcYmFye3h9X2kkKSBhbmQgd2l0aGluIChkZW1lYW5lZDsgJHhfe2l0fSAtIFxiYXJ7eH1faSQpIGNvZWZmaWNpZW50cy4gVGhlIGRlbWVhbmVkL3dpdGhpbiBjb2VmZmljaWVudHMgaW4gTW9kZWwgMyBhcmUgaWRlbnRpY2FsIHRvIHRoZSBmaXhlZCBlZmZlY3RzIGNvZWZmaWNpZW50cyBpbiBNb2RlbCAxLiBJZiByb3dzIGhhZCBiZWVuIGRyb3BwZWQgYmVjYXVzZSBvZiBsaXN0d2lzZSBkZWxldGlvbiAobGlrZSwgaWYgdGhlcmUgd2VyZSBtaXNzaW5nIHZhbHVlcyBpbiBvbmUgb2YgaW5kZXBlbmRlbnQgdmFyaWFibGVzKSwgdGhlIGNvZWZmaWNpZW50cyB3b3VsZCBiZSBzbGlnaHRseSBvZmYsIHNpbmNlIHRoZSBkZW1lYW5lZCB2YWx1ZXMgd291bGQgaGF2ZSBiZWVuIGJhc2VkIG9uIGdyb3VwIG1lYW5zIHRoYXQgaW5jbHVkZWQgdGhlIHZhbHVlcyB0aGF0IHdlcmUgZHJvcHBlZCAoZS5nLiBhbGwgMjAxMyByb3dzIGFyZSBkcm9wcGVkIGJlY2F1c2Ugb2YgbGFncywgYnV0IHRoZSBncm91cCBtZWFucyBpbmNsdWRlZCAyMDEzKS4gVGhpcyBpc24ndCAgYSBwcm9ibGVtIGluIHRoZXNlIHJlZHVjZWQgbW9kZWxzLCBidXQgdGhhdCdzIG9uZSByZWFzb24gd2UgaW1wdXRlIGFsbCB0aGUgZGF0YeKAlHdlIG5lZWQgdGhlIGRhdGEgdG8gYmUgYXMgY29tcGxldGUgYXMgcG9zc2libGUgdG8gZ2V0IHRoZSBtb3N0IGFjY3VyYXRlIHJhbmRvbSBlZmZlY3RzLgoKYGBge3IgZml4ZWQtcmFuZG9tLWV4YW1wbGUsIHdhcm5pbmc9RkFMU0UsIG1lc3NhZ2U9RkFMU0UsIHJlc3VsdHM9ImFzaXMifQptb2QudGVzdC5mZSA8LSBsbSh0b3RhbC5vZGFfbG9nX25leHRfeWVhciB+IGJhcnJpZXJzLnRvdGFsICsgcG9saXR5ICsgCiAgICAgICAgICAgICAgICAgICAgYXMuZmFjdG9yKGNvd2NvZGUpLAogICAgICAgICAgICAgICAgICBkYXRhID0gZGYuY291bnRyeS5haWQuZGVtZWFuLm5leHRfeWVhcikKCm1vZC50ZXN0LnJlIDwtIGxtZXIodG90YWwub2RhX2xvZ19uZXh0X3llYXIgfiBiYXJyaWVycy50b3RhbCArIHBvbGl0eSArIAogICAgICAgICAgICAgICAgICAgICAgKDEgfCBjb3djb2RlKSwKICAgICAgICAgICAgICAgICAgICBkYXRhID0gZGYuY291bnRyeS5haWQuZGVtZWFuLm5leHRfeWVhcikKCm1vZC50ZXN0LnJlLmZhbmN5IDwtIGxtZXIodG90YWwub2RhX2xvZ19uZXh0X3llYXIgfiAKICAgICAgICAgICAgICAgICAgICAgICAgICAgIGJhcnJpZXJzLnRvdGFsX2JldHdlZW4gKyBiYXJyaWVycy50b3RhbF93aXRoaW4gKwogICAgICAgICAgICAgICAgICAgICAgICAgICAgcG9saXR5X2JldHdlZW4gKyBwb2xpdHlfd2l0aGluICsgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAoMSB8IGNvd2NvZGUpLAogICAgICAgICAgICAgICAgICAgICAgICAgIGRhdGEgPSBkZi5jb3VudHJ5LmFpZC5kZW1lYW4ubmV4dF95ZWFyKQoKIyBNYWtlIG5hbWVkIGxpc3Qgb2YgY29lZmZpY2llbnRzIHRvIGluY2x1ZGUgaW4gdGhlIHRhYmxlCmFsbF9jb2VmcyA8LSBkYXRhX2ZyYW1lKG1vZGVsID0gbGlzdChtb2QudGVzdC5mZSwgbW9kLnRlc3QucmUsIG1vZC50ZXN0LnJlLmZhbmN5KSkgJT4lIAogIG11dGF0ZSh0aWR5ID0gbW9kZWwgJT4lIG1hcCh0aWR5KSkgJT4lIAogIHVubmVzdCh0aWR5KSAlPiUgCiAgZmlsdGVyKCFzdHJfZGV0ZWN0KHRlcm0sICJjb3djb2RlIiksIChlZmZlY3QgIT0gInJhbl9wYXJzIiB8IGlzLm5hKGVmZmVjdCkpKSAlPiUgCiAgZmlsdGVyKCFkdXBsaWNhdGVkKHRlcm0sIGZyb21MYXN0ID0gVFJVRSkpICU+JSAKICBmaWx0ZXIodGVybSAhPSAiKEludGVyY2VwdCkiKSAlPiUgCiAgbGVmdF9qb2luKGNvZWYubmFtZXMuYWxsLCBieSA9ICJ0ZXJtIikKICAKY29lZnNfbmFtZWQgPC0gYWxsX2NvZWZzICU+JSBwdWxsKHRlcm0pICU+JSAKICBzZXRfbmFtZXMoYWxsX2NvZWZzJHRlcm1fY2xlYW4pCgp0YmxfZXhhbXBsZSA8LSBodXhyZWcobW9kLnRlc3QuZmUsIG1vZC50ZXN0LnJlLCBtb2QudGVzdC5yZS5mYW5jeSwgCiAgICAgICAgICAgICAgICAgICAgICBjb2VmcyA9IGMoY29lZnNfbmFtZWQsIENvbnN0YW50ID0gIihJbnRlcmNlcHQpIiksCiAgICAgICAgICAgICAgICAgICAgICBzdGFycyA9IE5VTEwsIHN0YXRpc3RpY3MgPSBjKE4gPSAibm9icyIpLCBub3RlID0gIiIpICU+JSAKICBpbnNlcnRfcm93KGMoIkNvdW50cnkgZWZmZWN0cyIsICJGaXhlZCIsICJSYW5kb20iLCAiUmFuZG9tIiksCiAgICAgICAgICAgICBhZnRlciA9IG5yb3coLikgLSAyLCBjb3B5X2NlbGxfcHJvcHMgPSBGQUxTRSkgJT4lIAogICMgSGlnaGxpZ2h0IGlkZW50aWNhbCBjZWxscwogIHNldF9ib2xkKDI6NSwgMiwgVFJVRSkgJT4lIAogIHNldF9ib2xkKGMoOCwgOSwgMTIsIDEzKSwgNCwgVFJVRSkKCnRibF9leGFtcGxlICU+JSBwcmludF9odXgoKQoKdGJsX2V4YW1wbGUgJT4lIAogIHRvX21kKG1heF93aWR0aCA9IDEwMCkgJT4lIAogIGNhdChmaWxlID0gaGVyZSgiT3V0cHV0IiwgInRibC13aXRoaW4tYmV0d2Vlbi1leGFtcGxlLm1kIikpCmBgYAoKXApBbGwgb2YgdGhlIG1vZGVscyB3ZSBydW4gdXNlIGltcHV0ZWQgZGF0YSAoJG0gPSA1JCkgd2l0aCBjcm9zc2VkIHllYXIgYW5kIGNvdW50cnkgcmFuZG9tIGVmZmVjdHMuIE1vc3QgZXhwbGFuYXRvcnkgYW5kIGNvbnRyb2wgdmFyaWFibGVzIGFyZSBpbmNsdWRlZCBpbiB0aGVpciBtZWFuZWQgYW5kIGRlbWVhbmVkIGZvcm1zLCBleGNlcHQgZm9yIGFueSBpbmRpY2F0b3IgdmFyaWFibGVzIChzaW5jZSB5b3UgY2FuJ3QgcmVhbGx5IGF2ZXJhZ2UgYmluYXJ5IGRhdGEpLiBBZGRpdGlvbmFsbHksIHdlIGluY2x1ZGUgdGhlIHJlZ3VsYXIgZm9ybSBvZiB0aGUgY3VycmVudCB5ZWFyJ3MgT0RBIHRvIGFjY291bnQgZm9yIHRlbXBvcmFsIGF1dG9jb3JyZWxhdGlvbiBpbiBhaWQuIFdlIGRvIG5vdCBzcGxpdCBjdXJyZW50IE9EQSBpbnRvIHdpdGhpbiBhbmQgYmV0d2VlbiB2ZXJzaW9ucyBzbyB0aGF0IG1hdGhlbWF0aWNhbGx5IGl0IGNhbiBiZSBzdWJ0cmFjdGVkIG91dCBvZiB0aGUgbmV4dCB5ZWFyJ3MgT0RBIGluIHRoZSBkZXBlbmRlbnQgdmFyaWFibGUuIE90aGVyIG1peGVkIG1vZGVscyBmdW5jdGlvbnMgbGlrZSBgbmxtZTo6bG1lKClgIGFsbG93IHlvdSB0byBkZWZpbmUgYXV0b3JlZ3Jlc3NpdmUgY29ycmVsYXRpb24gc3RydWN0dXJlcywgYnV0IGBsbWU0OjpsbWVyKClgIGRvZXNuJ3QsIHNvIHdlIGFjY291bnQgZm9yIHRpbWUgd2l0aCB0aGlzIGRpZmZlcmVuY2VkIGFwcHJvYWNoIGluc3RlYWQuIEl0J3Mgbm90IHBlcmZlY3QsIGJ1dCBpdCB3b3JrczoKCmBgYHtyIHNob3cuYWNmLmxhZ3N9Cm1vZC50ZXN0Lm5vLm9kYSA8LSBsbWVyKHRvdGFsLm9kYV9sb2dfbmV4dF95ZWFyIH4gCiAgICAgICAgICAgICAgICAgICAgICAgICAgYmFycmllcnMudG90YWxfYmV0d2VlbiArIGJhcnJpZXJzLnRvdGFsX3dpdGhpbiArCiAgICAgICAgICAgICAgICAgICAgICAgICAgcG9saXR5X2JldHdlZW4gKyBwb2xpdHlfd2l0aGluICsgCiAgICAgICAgICAgICAgICAgICAgICAgICAgZ2RwLmNhcGl0YV9sb2dfYmV0d2VlbiArIGdkcC5jYXBpdGFfbG9nX3dpdGhpbiArCiAgICAgICAgICAgICAgICAgICAgICAgICAgKDEgfCBjb3djb2RlKSArICgxIHwgeWVhciksCiAgICAgICAgICAgICAgICAgICAgICAgIGRhdGEgPSBmaWx0ZXIoZGYuY291bnRyeS5haWQuZGVtZWFuLm5leHRfeWVhci5pbXB1dGUsCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgbSA9PSAiaW1wMSIpKQoKbW9kLnRlc3Qub2RhLnNwbGl0IDwtIGxtZXIodG90YWwub2RhX2xvZ19uZXh0X3llYXIgfiAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICBiYXJyaWVycy50b3RhbF9iZXR3ZWVuICsgYmFycmllcnMudG90YWxfd2l0aGluICsKICAgICAgICAgICAgICAgICAgICAgICAgICAgICBwb2xpdHlfYmV0d2VlbiArIHBvbGl0eV93aXRoaW4gKyAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICB0b3RhbC5vZGFfbG9nX2JldHdlZW4gKyB0b3RhbC5vZGFfbG9nX3dpdGhpbiArCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgZ2RwLmNhcGl0YV9sb2dfYmV0d2VlbiArIGdkcC5jYXBpdGFfbG9nX3dpdGhpbiArCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgKDEgfCBjb3djb2RlKSArICgxIHwgeWVhciksCiAgICAgICAgICAgICAgICAgICAgICAgICAgIGRhdGEgPSBmaWx0ZXIoZGYuY291bnRyeS5haWQuZGVtZWFuLm5leHRfeWVhci5pbXB1dGUsCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgbSA9PSAiaW1wMSIpKQoKbW9kLnRlc3Qub2RhLm5vc3BsaXQgPC0gbG1lcih0b3RhbC5vZGFfbG9nX25leHRfeWVhciB+IAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgYmFycmllcnMudG90YWxfYmV0d2VlbiArIGJhcnJpZXJzLnRvdGFsX3dpdGhpbiArCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICBwb2xpdHlfYmV0d2VlbiArIHBvbGl0eV93aXRoaW4gKyAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIHRvdGFsLm9kYV9sb2cgKwogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgZ2RwLmNhcGl0YV9sb2dfYmV0d2VlbiArIGdkcC5jYXBpdGFfbG9nX3dpdGhpbiArCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAoMSB8IGNvd2NvZGUpICsgKDEgfCB5ZWFyKSwKICAgICAgICAgICAgICAgICAgICAgICAgICAgICBkYXRhID0gZmlsdGVyKGRmLmNvdW50cnkuYWlkLmRlbWVhbi5uZXh0X3llYXIuaW1wdXRlLAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgbSA9PSAiaW1wMSIpKQoKcmVzaWQubm8ub2RhIDwtIGFjZihyZXNpZHVhbHMobW9kLnRlc3Qubm8ub2RhKSwgcGxvdCA9IEZBTFNFKQpyZXNpZC5vZGEgPC0gYWNmKHJlc2lkdWFscyhtb2QudGVzdC5vZGEubm9zcGxpdCksIHBsb3QgPSBGQUxTRSkKCmNpLmxpbmUgPC0gcW5vcm0oKDEgKyAwLjk1KSAvIDIpIC8gc3FydChyZXNpZC5uby5vZGEkbi51c2VkKQoKYWNmLnBsb3QuZGF0YSA8LSBiaW5kX3Jvd3MoCiAgZGF0YV9mcmFtZShMYWcgPSByZXNpZC5uby5vZGEkbGFnWywsMV0sIEFDRiA9IHJlc2lkLm5vLm9kYSRhY2ZbLCwxXSwgCiAgICAgICAgICAgICBtb2RlbCA9ICJObyBPREEiKSwKICBkYXRhX2ZyYW1lKExhZyA9IHJlc2lkLm9kYSRsYWdbLCwxXSwgQUNGID0gcmVzaWQub2RhJGFjZlssLDFdLCAKICAgICAgICAgICAgIG1vZGVsID0gIkN1cnJlbnQgeWVhcuKAmXMgT0RBIikKKQoKZ2dwbG90KGFjZi5wbG90LmRhdGEsIGFlcyh4ID0gTGFnLCB5ID0gQUNGLCBmaWxsID0gbW9kZWwpKSArCiAgZ2VvbV9iYXIoc3RhdCA9ICJpZGVudGl0eSIsIHBvc2l0aW9uID0gcG9zaXRpb25fZG9kZ2Uod2lkdGggPSAxKSwgd2lkdGggPSAwLjUpICsKICBnZW9tX2hsaW5lKHlpbnRlcmNlcHQgPSAwLCBzaXplID0gMSkgKwogIGdlb21faGxpbmUoeWludGVyY2VwdCA9IGMoY2kubGluZSwgLWNpLmxpbmUpLCBzaXplID0gMC41LCBsaW5ldHlwZSA9ICJkYXNoZWQiKSArCiAgZ3VpZGVzKGZpbGwgPSBndWlkZV9sZWdlbmQodGl0bGUgPSBOVUxMKSkgKwogIHRoZW1lX2Rvbm9ycygpCmBgYAoKTm90IHNwbGl0dGluZyBjdXJyZW50IE9EQSBpbnRvIHdpdGhpbiBhbmQgYmV0d2VlbiBhbHNvIGZpeGVzIGFub3RoZXIgc3RpY2t5IG1hdGhlbWF0aWNhbCBpc3N1ZS4gV2hlbiB0aGUgbW9kZWxzIGFyZSBydW4gd2l0aCB3aXRoaW4gYW5kIGN1cnJlbnQgT0RBLCB0aGUgJFxzaWdtYSQgdmFsdWUgZm9yIHdpdGhpbi1jb3VudHJ5IHZhcmlhYmlsaXR5IGJlY29tZXMgMCBmb3Igd2hhdGV2ZXIgcmVhc29uIChtYXliZSBpdCBzd2FsbG93cyB1cCB0b28gbXVjaCBjb3VudHJ5IGxldmVsIHZhcmlhYmlsaXR5PykuIFdoZW4gJFxzaWdtYSA9IDAkLCB0aGUgYmV0d2Vlbi1ncm91cCB2YXJpYWJpbGl0eSBpcyB0b28gc21hbGwgdG8gZnVsbHkgYWNjb3VudCBmb3IgYmV0d2VlbiBlZmZlY3RzLCByZXN1bHRpbmcgaW4gYSAiZGVnZW5lcmF0ZSBtb2RlbCIgKHNlZSBbcGFnZXMgMTDigJMxMSBoZXJlXShodHRwOi8vbG1lNC5yLWZvcmdlLnItcHJvamVjdC5vcmcvbE1Nd1IvbHJncHJ0LnBkZikpIGFuZCBpbmZsdWVuY2luZyB0aGUgY29lZmZpY2llbnRzIGluIHdlaXJkIHdheXMuIFNlZSBiZWxvdywgd2hlcmUgTW9kZWwgMSB1c2VzIHRoZSBzcGxpdCBjdXJyZW50IE9EQSBhbmQgTW9kZWwgMiBkb2Vzbid0OiAkXHNpZ21hJCBpbiBNb2RlbCAyIGV4aXN0cyBhbmQgdGhlIGNvZWZmaWNpZW50cyBhcmUgYmV0dGVyIGVzdGltYXRlZC4KCmBgYHtyIGgxLXRhYmxlLXJlc3VsdHMsIHJlc3VsdHM9ImFzaXMifQpodXhyZWcobW9kLnRlc3Qub2RhLnNwbGl0LCBtb2QudGVzdC5vZGEubm9zcGxpdCwKICAgICAgIHRpZHlfYXJncyA9IGxpc3QoZWZmZWN0cyA9ICJmaXhlZCIpLAogICAgICAgc3RhdGlzdGljcyA9IGMoTiA9ICJub2JzIikpCgpiaW5kX3Jvd3MoCiAgYXMuZGF0YS5mcmFtZShWYXJDb3JyKG1vZC50ZXN0Lm9kYS5zcGxpdCkpICU+JSBtdXRhdGUobW9kZWwgPSAiKDEpIiksCiAgYXMuZGF0YS5mcmFtZShWYXJDb3JyKG1vZC50ZXN0Lm9kYS5ub3NwbGl0KSkgJT4lIG11dGF0ZShtb2RlbCA9ICIoMikiKQopICU+JSAKICBtdXRhdGUoZ3JwID0gb3JkZXJlZChmY3RfaW5vcmRlcihncnApKSkgJT4lCiAgc2VsZWN0KGBSYW5kb20gdmFyaWFibGVgID0gZ3JwLCBzZGNvciwgbW9kZWwpICU+JQogIHNwcmVhZChtb2RlbCwgc2Rjb3IpICU+JSBwYW5kb2MudGFibGUoKQpgYGAKCi0tLQoKIyMgUmVzdWx0cwoKVGhlIHJlc3VsdHMgb2YgYWxsIG1vZGVscyBjYW4gYmUgZm91bmQgaW4gdGhlIFsiQmF5ZXNpYW4gbW9kZWxzIiBub3RlYm9va10obW9kZWxzLWJheWVzaWFuLmh0bWwpLCBzaW5jZSBpdCB0YWtlcyBzbyBtYW55IGhvdXJzIHRvIHJ1biB0aGVtIGFsbC4KCi0tLQoKIyMgU3VtbWFyeSBvZiBoeXBvdGhlc2VzCgpgYGB7ciBoeXBvdGhlc2VzLXN1bW1hcnksIHJlc3VsdHM9ImFzaXMiLCBtZXNzYWdlPUZBTFNFLCB3YXJuaW5nPUZBTFNFfQpmaW5kaW5ncy5zdW1tYXJ5IDwtIHJlYWRfY3N2KGhlcmUoIkRhdGEiLCAiZGF0YV9tYW51YWwiLCAiZmluZGluZ3Nfc3VtbWFyeS5jc3YiKSkKCmNhcHRpb24gPC0gIlN1bW1hcnkgb2YgZmluZGluZ3MgeyN0Ymw6ZmluZGluZ3Mtc3VtbWFyeX0iCmZpbmRpbmdzLnN1bW1hcnkudGFibGUgPC0gcGFuZG9jLnRhYmxlLnJldHVybihmaW5kaW5ncy5zdW1tYXJ5LCBqdXN0aWZ5ID0gImxsbCIsCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICBrZWVwLmxpbmUuYnJlYWtzID0gVFJVRSwgc3R5bGUgPSAiZ3JpZCIsCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICBjYXB0aW9uID0gY2FwdGlvbikKCmNhdChmaW5kaW5ncy5zdW1tYXJ5LnRhYmxlKQpjYXQoZmluZGluZ3Muc3VtbWFyeS50YWJsZSwgZmlsZSA9IGhlcmUoIk91dHB1dCIsICJ0YmwtZmluZGluZ3Mtc3VtbWFyeS5tZCIpKQpgYGAKCi0tLQoKIyMgUm9idXN0bmVzcyBjaGVja3MKCiMjIyBJbXB1dGF0aW9uCgpbQXMgZGlzY3Vzc2VkIG92ZXIgaW4gdGhlIGRhdGEgY2xlYW5pbmcgZmlsZV0oLi4vRGF0YS9nZXRfbWVyZ2VfZGF0YS5odG1sI21pc3NpbmduZXNzX2FuZF9pbXB1dGF0aW9uKSwgd2UgaW1wdXRlIGRhdGEgZm9yIHRoZSBmZXcgdmFyaWFibGVzIHRoYXQgYXJlIG1pc3NpbmcuIFRvIHNob3cgd2hhdCBkaWZmZXJlbmNlIGltcHV0YXRpb24gbWFrZXMsIHRoZSB0YWJsZSBiZWxvdyBzaG93cyB0aHJlZSBwYWlycyBvZiBtb2RlbHMgZnJvbSBIfjF+LiBUaGUgZmlyc3QgdHdvIG1vZGVscyBhcmUgcnVuIG9uIG5vbi1pbXB1dGVkIGRhdGEgKHNvIG1pc3Npbmcgb2JzZXJ2YXRpb25zIGFyZSBkZWxldGVkIGxpc3R3aXNlKSwgdGhlIHNlY29uZCB0d28gbW9kZWxzIGFyZSBydW4gb24gNSBzZXRzIG9mIGltcHV0ZWQgZGF0YSwgYW5kIHRoZSBsYXN0IHR3byBtb2RlbHMgYXJlIHJ1biBvbiAxMCBzZXRzIG9mIGltcHV0ZWQgZGF0YS4gCgpJdCdzIGNsZWFyIHRoYXQgaW1wdXRhdGlvbiBtYWtlcyBhIHN1YnN0YW50aWFsIGRpZmZlcmVuY2XigJRub3RlIHRoZSBiaWcgZGlmZmVyZW5jZXMgYmV0d2VlbiBjb2VmZmljaWVudHMuIEhvd2V2ZXIsIHRoZSBudW1iZXIgb2YgaW1wdXRlZCBkYXRhc2V0cyBkb2Vzbid0IHNlZW0gdG8gbWF0dGVyLCBzaW5jZSB0aGVyZSBhcmUgb25seSB0cml2aWFsIGRpZmZlcmVuY2VzIGluIGNvZWZmaWNpZW50cyB3aGVuIHRoZXJlIGFyZSA1IGFuZCAxMCBkYXRhc2V0cy4KCmBgYHtyIHJvYnVzdC1jb21wYXJlLWltcHV0YXRpb25zLCBtZXNzYWdlPUZBTFNFLCB3YXJuaW5nPUZBTFNFLCBjYWNoZT1UUlVFfQptb2RzLnJvYnVzdC5jaGVjay5tLm5leHRfeWVhci5yYXcgPC0gZGYuY291bnRyeS5haWQuZGVtZWFuLm5leHRfeWVhci5hbGwgJT4lCiAgbmVzdCgtbSkgJT4lCiAgbXV0YXRlKG1vZC5oMS5iYXJyaWVycy50b3RhbCA9IGRhdGEgJT4lIAogICAgICAgICAgIGZ1dHVyZV9tYXAobW9kLmgxLmJhcnJpZXJzLnRvdGFsLAogICAgICAgICAgICAgICAgICAgICAgInRvdGFsLm9kYV9sb2dfbmV4dF95ZWFyIiksCiAgICAgICAgIG1vZC5oMS50eXBlLnRvdGFsID0gZGF0YSAlPiUgCiAgICAgICAgICAgZnV0dXJlX21hcChtb2QuaDEudHlwZS50b3RhbCwKICAgICAgICAgICAgICAgICAgICAgICJ0b3RhbC5vZGFfbG9nX25leHRfeWVhciIpKQoKIyBHZXQgbW9kZWwgZGV0YWlscyBhbmQgcGFyYW1ldGVycwptb2RzLnJvYnVzdC5jaGVjay5tLm5leHRfeWVhciA8LSBtb2RzLnJvYnVzdC5jaGVjay5tLm5leHRfeWVhci5yYXcgJT4lCiAgZ2F0aGVyKG1vZGVsLm5hbWUsIG1vZGVsLCAtbSwgLWRhdGEpICU+JQogIG11dGF0ZShnbGFuY2UgPSBtb2RlbCAlPiUgbWFwKGJyb29tOjpnbGFuY2UpLAogICAgICAgICB0aWR5ID0gbW9kZWwgJT4lIG1hcChicm9vbTo6dGlkeSwgY29uZi5pbnQgPSBUUlVFKSkKCiMgTWVsZCB0aGUgaW1wdXRlZCBtb2RlbHMKbW9kcy5yb2J1c3QuY2hlY2subS5uZXh0X3llYXIubWVsZGVkLm9yaWdpbmFsIDwtIG1vZHMucm9idXN0LmNoZWNrLm0ubmV4dF95ZWFyICU+JQogIGZpbHRlcihtID09ICJvcmlnaW5hbCIpICU+JQogIGdyb3VwX2J5KG1vZGVsLm5hbWUpICU+JQogIG5lc3QoKSAlPiUKICBtdXRhdGUodGlkeS5tZWxkZWQgPSBkYXRhICU+JSBtYXAobWVsZC5pbXB1dGVkLm1vZGVscykpCgptb2RzLnJvYnVzdC5jaGVjay5tLm5leHRfeWVhci5tZWxkZWQubTUgPC0gbW9kcy5yb2J1c3QuY2hlY2subS5uZXh0X3llYXIgJT4lCiAgZmlsdGVyKG0gJWluJSBwYXN0ZTAoImltcCIsIDE6NSkpICU+JQogIGdyb3VwX2J5KG1vZGVsLm5hbWUpICU+JQogIG5lc3QoKSAlPiUKICBtdXRhdGUodGlkeS5tZWxkZWQgPSBkYXRhICU+JSBtYXAobWVsZC5pbXB1dGVkLm1vZGVscykpCgptb2RzLnJvYnVzdC5jaGVjay5tLm5leHRfeWVhci5tZWxkZWQubTEwIDwtIG1vZHMucm9idXN0LmNoZWNrLm0ubmV4dF95ZWFyICU+JQogIGZpbHRlcihtICE9ICJvcmlnaW5hbCIpICU+JQogIGdyb3VwX2J5KG1vZGVsLm5hbWUpICU+JQogIG5lc3QoKSAlPiUKICBtdXRhdGUodGlkeS5tZWxkZWQgPSBkYXRhICU+JSBtYXAobWVsZC5pbXB1dGVkLm1vZGVscykpCgptb2RzLnJvYnVzdC5jaGVjay5tLm5leHRfeWVhci5tZWxkZWQuYWxsIDwtIGJpbmRfcm93cygKICBtb2RzLnJvYnVzdC5jaGVjay5tLm5leHRfeWVhci5tZWxkZWQub3JpZ2luYWwsCiAgbW9kcy5yb2J1c3QuY2hlY2subS5uZXh0X3llYXIubWVsZGVkLm01LAogIG1vZHMucm9idXN0LmNoZWNrLm0ubmV4dF95ZWFyLm1lbGRlZC5tMTAKKSAlPiUKICBtdXRhdGUoaW1wdXRhdGlvbnMgPSBkYXRhICU+JSBtYXBfZGJsKH4gbnJvdyguKSksCiAgICAgICAgIG1vZGVsLm5hbWUgPSBwYXN0ZShtb2RlbC5uYW1lLCBpbXB1dGF0aW9ucywgc2VwID0gIl8iKSkKYGBgCgpgYGB7ciB0Ymwtc2hvdy1pbXB1dGF0aW9ucywgcmVzdWx0cz0iYXNpcyJ9CnN0YXJnYXplci5mYWtlKG1vZHMucm9idXN0LmNoZWNrLm0ubmV4dF95ZWFyLm1lbGRlZC5hbGwpICU+JSBjYXQoKQpgYGAKCiMjIyBOZXV0cmFsIHJlZ3VsYXRpb25zIHsudGFic2V0IC50YWJzZXQtZmFkZSAudGFic2V0LXBpbGxzfQoKYGBge3Igcm9idXN0LW5ldXRyYWwtcmVndWxhdGlvbnMsIGNhY2hlPVRSVUV9Cm1vZHMucm9idXN0Lm5ldXRyYWwucmVncy5yYXcgPC0gZGYuY291bnRyeS5haWQuZGVtZWFuLm5leHRfeWVhci5hbGwgJT4lCiAgbmVzdCgtbSkgJT4lCiAgbXV0YXRlKG1vZC5oMS5uZXV0cmFsLnJlZyA9IGRhdGEgJT4lIAogICAgICAgICAgIGZ1dHVyZV9tYXAobW9kLmgxLm5ldXRyYWwucmVnLAogICAgICAgICAgICAgICAgICAgICAgInRvdGFsLm9kYV9sb2dfbmV4dF95ZWFyIiksCiAgICAgICAgIG1vZC5oMS5uZXV0cmFsLmZ1bmQgPSBkYXRhICU+JSAKICAgICAgICAgICBmdXR1cmVfbWFwKG1vZC5oMS5uZXV0cmFsLmZ1bmQsCiAgICAgICAgICAgICAgICAgICAgICAidG90YWwub2RhX2xvZ19uZXh0X3llYXIiKSwKICAgICAgICAgbW9kLmgyLm5ldXRyYWwucmVnID0gZGF0YSAlPiUgCiAgICAgICAgICAgZnV0dXJlX21hcChtb2QuaDIubmV1dHJhbC5yZWcsCiAgICAgICAgICAgICAgICAgICAgICAicHJvcC5jb250ZW50aW91c19sb2dpdF9uZXh0X3llYXIiKSwKICAgICAgICAgbW9kLmgyLm5ldXRyYWwuZnVuZCA9IGRhdGEgJT4lIAogICAgICAgICAgIGZ1dHVyZV9tYXAobW9kLmgyLm5ldXRyYWwuZnVuZCwKICAgICAgICAgICAgICAgICAgICAgICJwcm9wLmNvbnRlbnRpb3VzX2xvZ2l0X25leHRfeWVhciIpKQoKbW9kcy5yb2J1c3QubmV1dHJhbC5yZWdzLnJhdy5oMyA8LSBkZi5jb3VudHJ5LmFpZC51cy5kZW1lYW4ubmV4dF95ZWFyLmJvdGggJT4lCiAgbmVzdCgtbSkgJT4lCiAgbXV0YXRlKG1vZC5oMy5kb20ubmV1dHJhbC5yZWcgPSBkYXRhICU+JSAKICAgICAgICAgICBmdXR1cmVfbWFwKG1vZC5oMy5kb20ubmV1dHJhbC5yZWcsCiAgICAgICAgICAgICAgICAgICAgICAicHJvcC5uZ28uZG9tX2xvZ2l0X25leHRfeWVhciIpLAogICAgICAgICBtb2QuaDMuZG9tLm5ldXRyYWwuZnVuZCA9IGRhdGEgJT4lIAogICAgICAgICAgIGZ1dHVyZV9tYXAobW9kLmgzLmRvbS5uZXV0cmFsLmZ1bmQsCiAgICAgICAgICAgICAgICAgICAgICAicHJvcC5uZ28uZG9tX2xvZ2l0X25leHRfeWVhciIpLAogICAgICAgICBtb2QuaDMuZm9yLm5ldXRyYWwucmVnID0gZGF0YSAlPiUgCiAgICAgICAgICAgZnV0dXJlX21hcChtb2QuaDMuZm9yLm5ldXRyYWwucmVnLAogICAgICAgICAgICAgICAgICAgICAgInByb3AubmdvLmZvcmVpZ25fbG9naXRfbmV4dF95ZWFyIiksCiAgICAgICAgIG1vZC5oMy5mb3IubmV1dHJhbC5mdW5kID0gZGF0YSAlPiUgCiAgICAgICAgICAgZnV0dXJlX21hcChtb2QuaDMuZm9yLm5ldXRyYWwuZnVuZCwKICAgICAgICAgICAgICAgICAgICAgICJwcm9wLm5nby5mb3JlaWduX2xvZ2l0X25leHRfeWVhciIpKQoKIyBHZXQgbW9kZWwgZGV0YWlscyBhbmQgcGFyYW1ldGVycwptb2RzLnJvYnVzdC5uZXV0cmFsLnJlZ3MgPC0gbW9kcy5yb2J1c3QubmV1dHJhbC5yZWdzLnJhdyAlPiUKICBnYXRoZXIobW9kZWwubmFtZSwgbW9kZWwsIC1tLCAtZGF0YSkgJT4lCiAgbXV0YXRlKGdsYW5jZSA9IG1vZGVsICU+JSBtYXAoYnJvb206OmdsYW5jZSksCiAgICAgICAgIHRpZHkgPSBtb2RlbCAlPiUgbWFwKGJyb29tOjp0aWR5LCBjb25mLmludCA9IFRSVUUpKQoKbW9kcy5yb2J1c3QubmV1dHJhbC5yZWdzLmgzIDwtIG1vZHMucm9idXN0Lm5ldXRyYWwucmVncy5yYXcuaDMgJT4lCiAgZ2F0aGVyKG1vZGVsLm5hbWUsIG1vZGVsLCAtbSwgLWRhdGEpICU+JQogIG11dGF0ZShnbGFuY2UgPSBtb2RlbCAlPiUgbWFwKGJyb29tOjpnbGFuY2UpLAogICAgICAgICB0aWR5ID0gbW9kZWwgJT4lIG1hcChicm9vbTo6dGlkeSwgY29uZi5pbnQgPSBUUlVFKSkKCiMgTWVsZCB0aGUgaW1wdXRlZCBtb2RlbHMKbW9kcy5yb2J1c3QubmV1dHJhbC5yZWdzLm1lbGRlZC5oMSA8LSBtb2RzLnJvYnVzdC5uZXV0cmFsLnJlZ3MgJT4lCiAgZmlsdGVyKG0gIT0gIm9yaWdpbmFsIiwgc3RyX2RldGVjdChtb2RlbC5uYW1lLCAiaDEiKSkgJT4lCiAgZ3JvdXBfYnkobW9kZWwubmFtZSkgJT4lCiAgbmVzdCgpICU+JQogIG11dGF0ZSh0aWR5Lm1lbGRlZCA9IGRhdGEgJT4lIG1hcChtZWxkLmltcHV0ZWQubW9kZWxzKSkKCm1vZHMucm9idXN0Lm5ldXRyYWwucmVncy5tZWxkZWQuaDIgPC0gbW9kcy5yb2J1c3QubmV1dHJhbC5yZWdzICU+JQogIGZpbHRlcihtICE9ICJvcmlnaW5hbCIsIHN0cl9kZXRlY3QobW9kZWwubmFtZSwgImgyIikpICU+JQogIGdyb3VwX2J5KG1vZGVsLm5hbWUpICU+JQogIG5lc3QoKSAlPiUKICBtdXRhdGUodGlkeS5tZWxkZWQgPSBkYXRhICU+JSBtYXAofiBtZWxkLmltcHV0ZWQubW9kZWxzKC4sIGV4cG9uZW50aWF0ZSA9IFRSVUUpKSkKCm1vZHMucm9idXN0Lm5ldXRyYWwucmVncy5tZWxkZWQuaDMgPC0gbW9kcy5yb2J1c3QubmV1dHJhbC5yZWdzLmgzICU+JQogIGZpbHRlcihtICE9ICJvcmlnaW5hbCIpICU+JQogIGdyb3VwX2J5KG1vZGVsLm5hbWUpICU+JQogIG5lc3QoKSAlPiUKICBtdXRhdGUodGlkeS5tZWxkZWQgPSBkYXRhICU+JSBtYXAofiBtZWxkLmltcHV0ZWQubW9kZWxzKC4sIGV4cG9uZW50aWF0ZSA9IFRSVUUpKSkKYGBgCgojIyMjIE5ldXRyYWwgcmVndWxhdGlvbnMgYW5kIG92ZXJhbGwgYWlkIChIMSkKCmBgYHtyIHRibC1zaG93LW5ldXRyYWwtaDEsIHJlc3VsdHM9ImFzaXMifQp0YWJsZS5yb2J1c3QubmV1dHJhbC5yZWdzLmgxIDwtIG1vZHMucm9idXN0Lm5ldXRyYWwucmVncy5tZWxkZWQuaDEgJT4lCiAgc3RhcmdhemVyLmZha2UoZXhwb25lbnRpYXRlID0gRkFMU0UpICU+JQogIGNhdCgpCmBgYAoKIyMjIyBOZXV0cmFsIHJlZ3VsYXRpb25zIGFuZCB0YW1lciBjYXVzZXMgKEgyKQoKYGBge3IgdGJsLXNob3ctbmV1dHJhbC1oMiwgcmVzdWx0cz0iYXNpcyJ9CnRhYmxlLnJvYnVzdC5uZXV0cmFsLnJlZ3MuaDIgPC0gbW9kcy5yb2J1c3QubmV1dHJhbC5yZWdzLm1lbGRlZC5oMiAlPiUKICBmaWx0ZXIoc3RyX2RldGVjdChtb2RlbC5uYW1lLCAiaDIiKSkgJT4lCiAgc3RhcmdhemVyLmZha2UoZXhwb25lbnRpYXRlID0gVFJVRSkgJT4lCiAgY2F0KCkKYGBgCgojIyMjIE5ldXRyYWwgcmVndWxhdGlvbnMgYW5kIE5HT3MgKEgzKQoKYGBge3IgdGJsLXNob3ctbmV1dHJhbC1oMywgcmVzdWx0cz0iYXNpcyJ9CnRhYmxlLnJvYnVzdC5uZXV0cmFsLnJlZ3MuaDMgPC0gbW9kcy5yb2J1c3QubmV1dHJhbC5yZWdzLm1lbGRlZC5oMyAlPiUKICBzdGFyZ2F6ZXIuZmFrZShleHBvbmVudGlhdGUgPSBUUlVFKSAlPiUKICBjYXQoKQpgYGAKCgojIyMgTG9uZ2VyIGxhZ3M6IEh+MX4gey50YWJzZXQgLnRhYnNldC1mYWRlIC50YWJzZXQtcGlsbHN9CgpMb29raW5nIGF0IGFpZCAyIHllYXJzIGFuZCA1IHllYXJzIGFmdGVyIHRoZSBjaGFuZ2UgaW4gYW50aS1OR08gbGVnaXNsYXRpb24gc2hvd3Mgc2ltaWxhciB0cmVuZHMgdG8gMSB5ZWFyIGFmdGVyLgoKYGBge3IgaDEtbW9kZWxzLTIsIHdhcm5pbmc9RkFMU0UsIG1lc3NhZ2U9RkFMU0UsIGNhY2hlPVRSVUV9Cm1vZHMuaDEuYWZ0ZXJfMi5yYXcgPC0gZGYuY291bnRyeS5haWQuZGVtZWFuLmFmdGVyXzIuaW1wdXRlICU+JQogIG5lc3QoLW0pICU+JQogIG11dGF0ZShtb2QuaDEuYmFycmllcnMudG90YWwgPSBkYXRhICU+JSAKICAgICAgICAgICBmdXR1cmVfbWFwKG1vZC5oMS5iYXJyaWVycy50b3RhbCwgInRvdGFsLm9kYV9sb2dfbmV4dF95ZWFyIiksCiAgICAgICAgIG1vZC5oMS50eXBlLnRvdGFsID0gZGF0YSAlPiUgCiAgICAgICAgICAgZnV0dXJlX21hcChtb2QuaDEudHlwZS50b3RhbCwgInRvdGFsLm9kYV9sb2dfbmV4dF95ZWFyIiksCiAgICAgICAgIG1vZC5oMS5jc3JlID0gZGF0YSAlPiUgCiAgICAgICAgICAgZnV0dXJlX21hcChtb2QuaDEuY3NyZSwgInRvdGFsLm9kYV9sb2dfbmV4dF95ZWFyIikpCgojIEdldCBtb2RlbCBkZXRhaWxzIGFuZCBwYXJhbWV0ZXJzCm1vZHMuaDEuYWZ0ZXJfMiA8LSBtb2RzLmgxLmFmdGVyXzIucmF3ICU+JQogIGdhdGhlcihtb2RlbC5uYW1lLCBtb2RlbCwgLW0sIC1kYXRhKSAlPiUKICBtdXRhdGUoZ2xhbmNlID0gbW9kZWwgJT4lIG1hcChicm9vbTo6Z2xhbmNlKSwKICAgICAgICAgdGlkeSA9IG1vZGVsICU+JSBtYXAoYnJvb206OnRpZHksIGNvbmYuaW50ID0gVFJVRSkpCgojIE1lbGQgdGhlIGltcHV0ZWQgbW9kZWxzCm1vZHMuaDEuYWZ0ZXJfMi5tZWxkZWQgPC0gbW9kcy5oMS5hZnRlcl8yICU+JQogIGZpbHRlcihtICE9ICJvcmlnaW5hbCIpICU+JQogIGdyb3VwX2J5KG1vZGVsLm5hbWUpICU+JQogIG5lc3QoKSAlPiUKICBtdXRhdGUodGlkeS5tZWxkZWQgPSBkYXRhICU+JSBtYXAobWVsZC5pbXB1dGVkLm1vZGVscykpCmBgYAoKYGBge3IgaDEtbW9kZWxzLTUsIHdhcm5pbmc9RkFMU0UsIG1lc3NhZ2U9RkFMU0UsIGNhY2hlPVRSVUV9Cm1vZHMuaDEuYWZ0ZXJfNS5yYXcgPC0gZGYuY291bnRyeS5haWQuZGVtZWFuLmFmdGVyXzUuaW1wdXRlICU+JQogIG5lc3QoLW0pICU+JQogIG11dGF0ZShtb2QuaDEuYmFycmllcnMudG90YWwgPSBkYXRhICU+JSAKICAgICAgICAgICBmdXR1cmVfbWFwKG1vZC5oMS5iYXJyaWVycy50b3RhbCwgInRvdGFsLm9kYV9sb2dfbmV4dF95ZWFyIiksCiAgICAgICAgIG1vZC5oMS50eXBlLnRvdGFsID0gZGF0YSAlPiUgCiAgICAgICAgICAgZnV0dXJlX21hcChtb2QuaDEudHlwZS50b3RhbCwgInRvdGFsLm9kYV9sb2dfbmV4dF95ZWFyIiksCiAgICAgICAgIG1vZC5oMS5jc3JlID0gZGF0YSAlPiUgCiAgICAgICAgICAgZnV0dXJlX21hcChtb2QuaDEuY3NyZSwgInRvdGFsLm9kYV9sb2dfbmV4dF95ZWFyIikpCgojIEdldCBtb2RlbCBkZXRhaWxzIGFuZCBwYXJhbWV0ZXJzCm1vZHMuaDEuYWZ0ZXJfNSA8LSBtb2RzLmgxLmFmdGVyXzUucmF3ICU+JQogIGdhdGhlcihtb2RlbC5uYW1lLCBtb2RlbCwgLW0sIC1kYXRhKSAlPiUKICBtdXRhdGUoZ2xhbmNlID0gbW9kZWwgJT4lIG1hcChicm9vbTo6Z2xhbmNlKSwKICAgICAgICAgdGlkeSA9IG1vZGVsICU+JSBtYXAoYnJvb206OnRpZHksIGNvbmYuaW50ID0gVFJVRSkpCgojIE1lbGQgdGhlIGltcHV0ZWQgbW9kZWxzCm1vZHMuaDEuYWZ0ZXJfNS5tZWxkZWQgPC0gbW9kcy5oMS5hZnRlcl81ICU+JQogIGZpbHRlcihtICE9ICJvcmlnaW5hbCIpICU+JQogIGdyb3VwX2J5KG1vZGVsLm5hbWUpICU+JQogIG5lc3QoKSAlPiUKICBtdXRhdGUodGlkeS5tZWxkZWQgPSBkYXRhICU+JSBtYXAobWVsZC5pbXB1dGVkLm1vZGVscykpCmBgYAoKIyMjIyBFZmZlY3Qgb24gT0RBIGFmdGVyIDIgeWVhcnMKCmBgYHtyIGgxLW1lbGRlZC10YWJsZS0yLCByZXN1bHRzPSJhc2lzIiwgd2FybmluZz1GQUxTRX0Kc3RhcmdhemVyLmZha2UobW9kcy5oMS5hZnRlcl8yLm1lbGRlZCkgJT4lIGNhdCgpCmBgYAoKIyMjIyBFZmZlY3Qgb24gT0RBIGFmdGVyIDUgeWVhcnMKCmBgYHtyIGgxLW1lbGRlZC10YWJsZS01LCByZXN1bHRzPSJhc2lzIiwgd2FybmluZz1GQUxTRX0Kc3RhcmdhemVyLmZha2UobW9kcy5oMS5hZnRlcl81Lm1lbGRlZCkgJT4lIGNhdCgpCmBgYAoKCiMjIyBMb25nZXIgbGFnczogSH4yfiB7LnRhYnNldCAudGFic2V0LWZhZGUgLnRhYnNldC1waWxsc30KCmBgYHtyIGgyLW1vZGVscy0yLCB3YXJuaW5nPUZBTFNFLCBtZXNzYWdlPUZBTFNFLCBjYWNoZT1UUlVFfQptb2RzLmgyLmFmdGVyXzIucmF3IDwtIGRmLmNvdW50cnkuYWlkLmRlbWVhbi5hZnRlcl8yLmltcHV0ZSAlPiUKICBuZXN0KC1tKSAlPiUKICBtdXRhdGUobW9kLmgyLmJhcnJpZXJzLnRvdGFsID0gZGF0YSAlPiUgCiAgICAgICAgICAgZnV0dXJlX21hcChtb2QuaDIuYmFycmllcnMudG90YWwsICJwcm9wLmNvbnRlbnRpb3VzX2xvZ2l0X25leHRfeWVhciIpLAogICAgICAgICBtb2QuaDIudHlwZS50b3RhbCA9IGRhdGEgJT4lIAogICAgICAgICAgIGZ1dHVyZV9tYXAobW9kLmgyLnR5cGUudG90YWwsICJwcm9wLmNvbnRlbnRpb3VzX2xvZ2l0X25leHRfeWVhciIpLAogICAgICAgICBtb2QuaDIuY3NyZSA9IGRhdGEgJT4lIAogICAgICAgICAgIGZ1dHVyZV9tYXAobW9kLmgyLmNzcmUsICJwcm9wLmNvbnRlbnRpb3VzX2xvZ2l0X25leHRfeWVhciIpKQoKIyBHZXQgbW9kZWwgZGV0YWlscyBhbmQgcGFyYW1ldGVycwptb2RzLmgyLmFmdGVyXzIgPC0gbW9kcy5oMi5hZnRlcl8yLnJhdyAlPiUKICBnYXRoZXIobW9kZWwubmFtZSwgbW9kZWwsIC1tLCAtZGF0YSkgJT4lCiAgbXV0YXRlKGdsYW5jZSA9IG1vZGVsICU+JSBtYXAoYnJvb206OmdsYW5jZSksCiAgICAgICAgIHRpZHkgPSBtb2RlbCAlPiUgbWFwKGJyb29tOjp0aWR5LCBjb25mLmludCA9IFRSVUUpKQoKIyBNZWxkIHRoZSBpbXB1dGVkIG1vZGVscwptb2RzLmgyLmFmdGVyXzIubWVsZGVkIDwtIG1vZHMuaDIuYWZ0ZXJfMiAlPiUKICBmaWx0ZXIobSAhPSAib3JpZ2luYWwiKSAlPiUKICBncm91cF9ieShtb2RlbC5uYW1lKSAlPiUKICBuZXN0KCkgJT4lCiAgbXV0YXRlKHRpZHkubWVsZGVkID0gZGF0YSAlPiUgbWFwKG1lbGQuaW1wdXRlZC5tb2RlbHMpKQpgYGAKCmBgYHtyIGgyLW1vZGVscy01LCB3YXJuaW5nPUZBTFNFLCBtZXNzYWdlPUZBTFNFLCBjYWNoZT1UUlVFfQptb2RzLmgyLmFmdGVyXzUucmF3IDwtIGRmLmNvdW50cnkuYWlkLmRlbWVhbi5hZnRlcl81LmltcHV0ZSAlPiUKICBuZXN0KC1tKSAlPiUKICBtdXRhdGUobW9kLmgyLmJhcnJpZXJzLnRvdGFsID0gZGF0YSAlPiUgCiAgICAgICAgICAgZnV0dXJlX21hcChtb2QuaDIuYmFycmllcnMudG90YWwsICJwcm9wLmNvbnRlbnRpb3VzX2xvZ2l0X25leHRfeWVhciIpLAogICAgICAgICBtb2QuaDIudHlwZS50b3RhbCA9IGRhdGEgJT4lIAogICAgICAgICAgIGZ1dHVyZV9tYXAobW9kLmgyLnR5cGUudG90YWwsICJwcm9wLmNvbnRlbnRpb3VzX2xvZ2l0X25leHRfeWVhciIpLAogICAgICAgICBtb2QuaDIuY3NyZSA9IGRhdGEgJT4lIAogICAgICAgICAgIGZ1dHVyZV9tYXAobW9kLmgyLmNzcmUsICJwcm9wLmNvbnRlbnRpb3VzX2xvZ2l0X25leHRfeWVhciIpKQoKIyBHZXQgbW9kZWwgZGV0YWlscyBhbmQgcGFyYW1ldGVycwptb2RzLmgyLmFmdGVyXzUgPC0gbW9kcy5oMi5hZnRlcl81LnJhdyAlPiUKICBnYXRoZXIobW9kZWwubmFtZSwgbW9kZWwsIC1tLCAtZGF0YSkgJT4lCiAgbXV0YXRlKGdsYW5jZSA9IG1vZGVsICU+JSBtYXAoYnJvb206OmdsYW5jZSksCiAgICAgICAgIHRpZHkgPSBtb2RlbCAlPiUgbWFwKGJyb29tOjp0aWR5LCBjb25mLmludCA9IFRSVUUpKQoKIyBNZWxkIHRoZSBpbXB1dGVkIG1vZGVscwptb2RzLmgyLmFmdGVyXzUubWVsZGVkIDwtIG1vZHMuaDIuYWZ0ZXJfNSAlPiUKICBmaWx0ZXIobSAhPSAib3JpZ2luYWwiKSAlPiUKICBncm91cF9ieShtb2RlbC5uYW1lKSAlPiUKICBuZXN0KCkgJT4lCiAgbXV0YXRlKHRpZHkubWVsZGVkID0gZGF0YSAlPiUgbWFwKG1lbGQuaW1wdXRlZC5tb2RlbHMpKQpgYGAKCiMjIyMgRWZmZWN0IG9uIGNvbnRlbnRpb3VzIGFpZCBhZnRlciAyIHllYXJzCgpgYGB7ciBoMi1tZWxkZWQtdGFibGUtMiwgcmVzdWx0cz0iYXNpcyIsIHdhcm5pbmc9RkFMU0V9CnN0YXJnYXplci5mYWtlKG1vZHMuaDIuYWZ0ZXJfMi5tZWxkZWQpICU+JSBjYXQoKQpgYGAKCiMjIyMgRWZmZWN0IG9uIGNvbnRlbnRpb3VzIGFpZCBhZnRlciA1IHllYXJzCgpgYGB7ciBoMi1tZWxkZWQtdGFibGUtNSwgcmVzdWx0cz0iYXNpcyIsIHdhcm5pbmc9RkFMU0V9CnN0YXJnYXplci5mYWtlKG1vZHMuaDIuYWZ0ZXJfNS5tZWxkZWQpICU+JSBjYXQoKQpgYGAK

Models

Suparna Chaudhry and Andrew Heiss

2018-10-29

Dependent variables

General model specifications and controls

Results

Summary of hypotheses

Robustness checks

Imputation

Neutral regulations

Neutral regulations and overall aid (H1)

Neutral regulations and tamer causes (H2)

Neutral regulations and NGOs (H3)

Longer lags: H₁

Effect on ODA after 2 years

Effect on ODA after 5 years

Longer lags: H₂

Effect on contentious aid after 2 years

Effect on contentious aid after 5 years

Models

Suparna Chaudhry and Andrew Heiss

2018-10-29

Dependent variables

General model specifications and controls

Results

Summary of hypotheses

Robustness checks

Imputation

Neutral regulations

Neutral regulations and overall aid (H1)

Neutral regulations and tamer causes (H2)

Neutral regulations and NGOs (H3)

Longer lags: H1

Effect on ODA after 2 years

Effect on ODA after 5 years

Longer lags: H2

Effect on contentious aid after 2 years

Effect on contentious aid after 5 years

Longer lags: H₁

Longer lags: H₂