Fancier analysis

Note: For now, this is all based on the BHL version of the simulation with landscape_fitness_linked as the outcome variable. That can all be changed, though.

---

library(tidyverse)
library(randomForest)
library(ggridges)
library(ggstance)
library(pander)
library(here)

# Load details about constraints
constraints <- read_rds(here("data", "derived_data", "constraints.rds"))

constraint_levels <- constraints %>%
  mutate(constraint_clean = fct_inorder(constraint_clean)) %>%
  mutate(levels = map(levels_clean, names)) %>%
  unnest(levels) %>%
  mutate(levels = fct_inorder(levels))

# Load simulation data
# TODO: Switch back to full BLS.rds and BHL.rds
BHL <- read_rds(here("data", "derived_data", "BHL_small.rds"))

sim_results <- BHL %>%
  # Make new columns with "_constraint" suffix that show if constraint is T/F
  # instead of using the label. e.g. "Selection" becomes TRUE, "No selection"
  # becomes FALSE
  mutate_at(vars(one_of(constraints$constraint)),
            list(constraint = ~as.logical(-as.integer(.) + 2L))) %>%
  # Count how many of the constraints are TRUE in each row
  mutate(n_constraints = reduce(select(., ends_with("_constraint")), `+`)) %>%
  # Make a factor version of the constraint count for plotting
  mutate(n_constraints_f = as.factor(n_constraints))

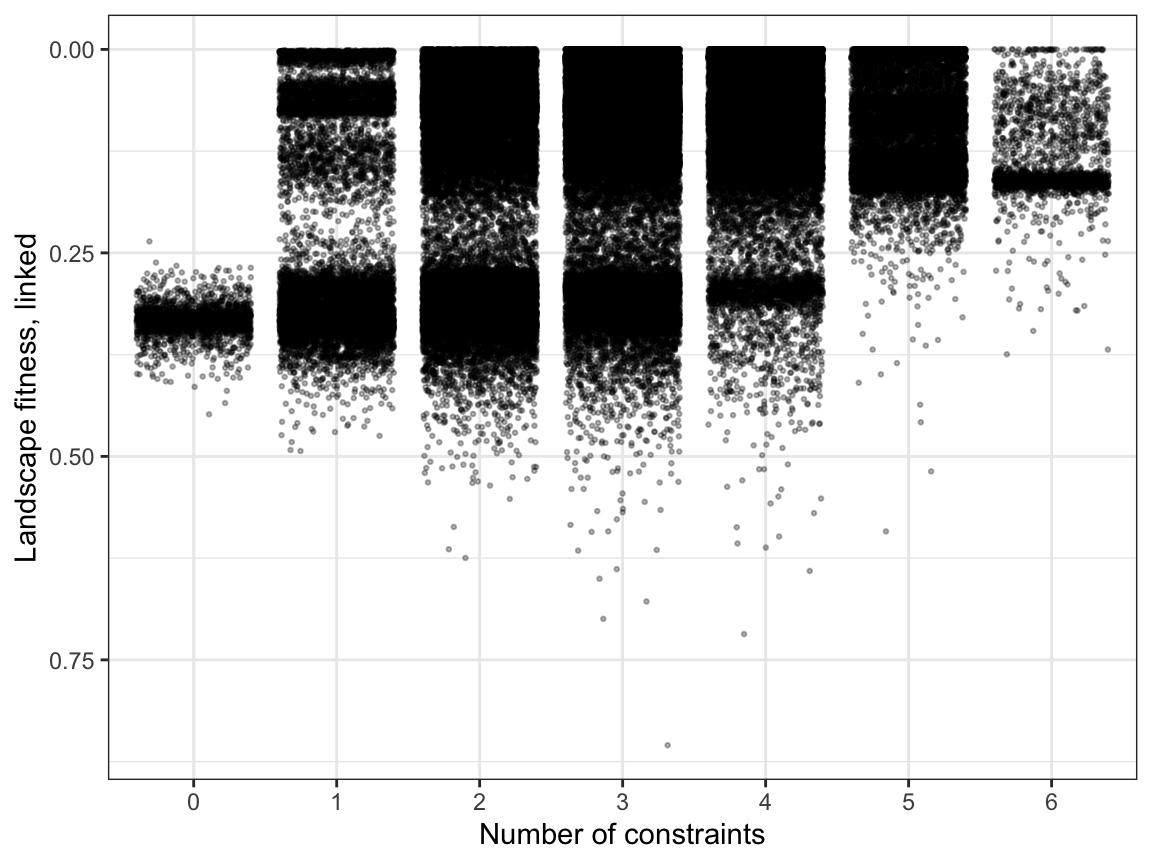
Average fitness as number of constraints increase

Points

Thanos apparently snapped this plot.

ggplot(sim_results, 
       aes(x = n_constraints_f, y = landscape_fitness_linked)) +
  geom_point(size = 0.5, alpha = 0.3, position = position_jitter(seed = 1234)) +
  scale_y_reverse() +
  labs(x = "Number of constraints",
       y = "Landscape fitness, linked") +
  theme_bw()

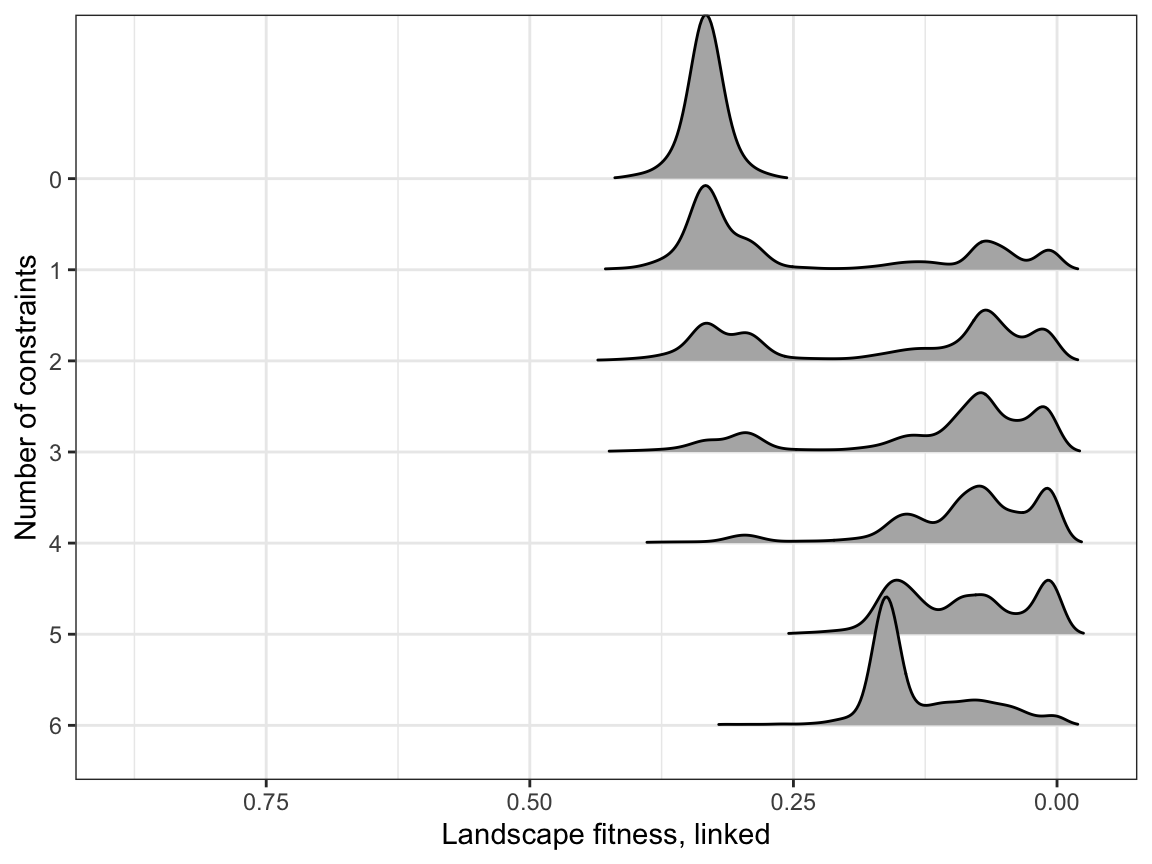
Ridges

ggplot(sim_results, 
       aes(x = landscape_fitness_linked, y = fct_rev(n_constraints_f))) +
  geom_density_ridges(rel_min_height = 0.005) +
  scale_x_reverse() +
  labs(x = "Landscape fitness, linked",
       y = "Number of constraints") +
  theme_bw()

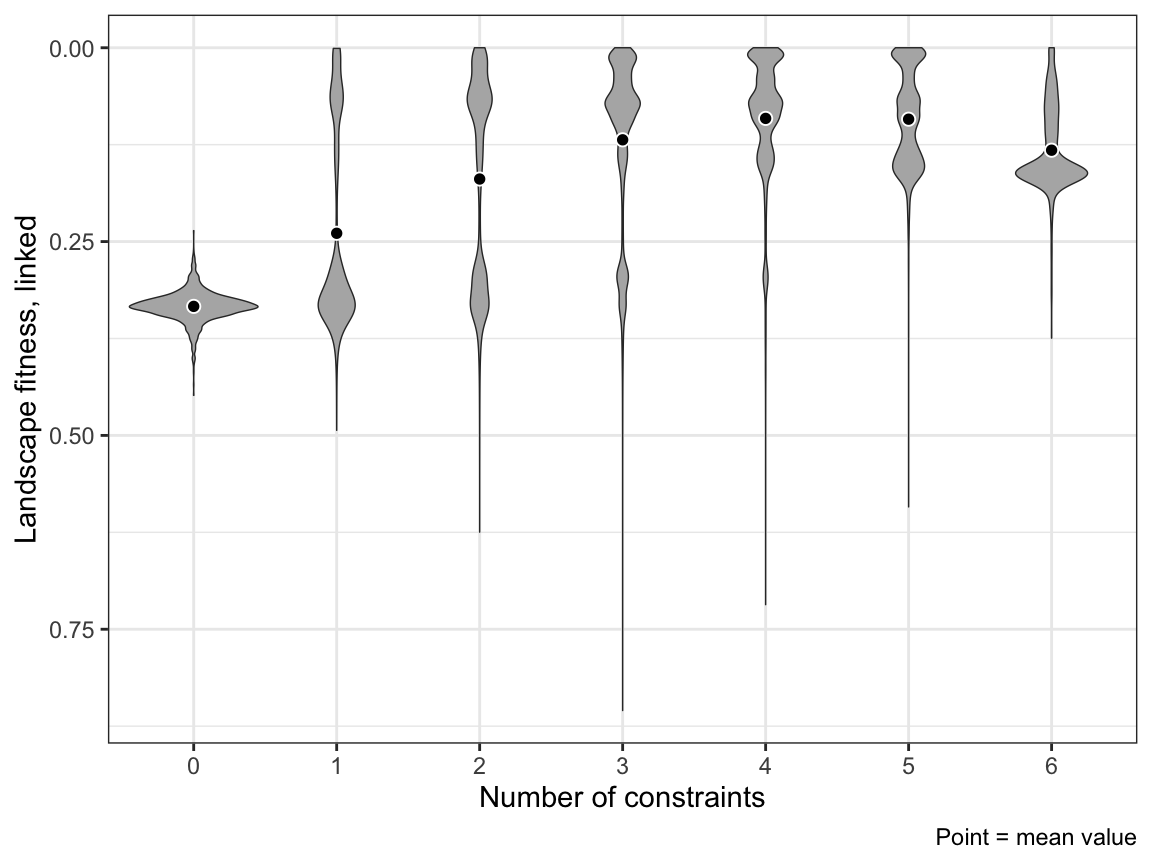
Violins

ggplot(sim_results, aes(x = n_constraints_f, y = landscape_fitness_linked)) +
  geom_violin(size = 0.25, fill = "grey70") +
  stat_summary(geom = "point", fun.y = "mean",
               size = 2, pch = 21, fill = "black", color = "white") +
  scale_y_reverse() +
  labs(x = "Number of constraints",
       y = "Landscape fitness, linked",
       caption = "Point = mean value") +
  theme_bw()

## Warning: `fun.y` is deprecated. Use `fun` instead.

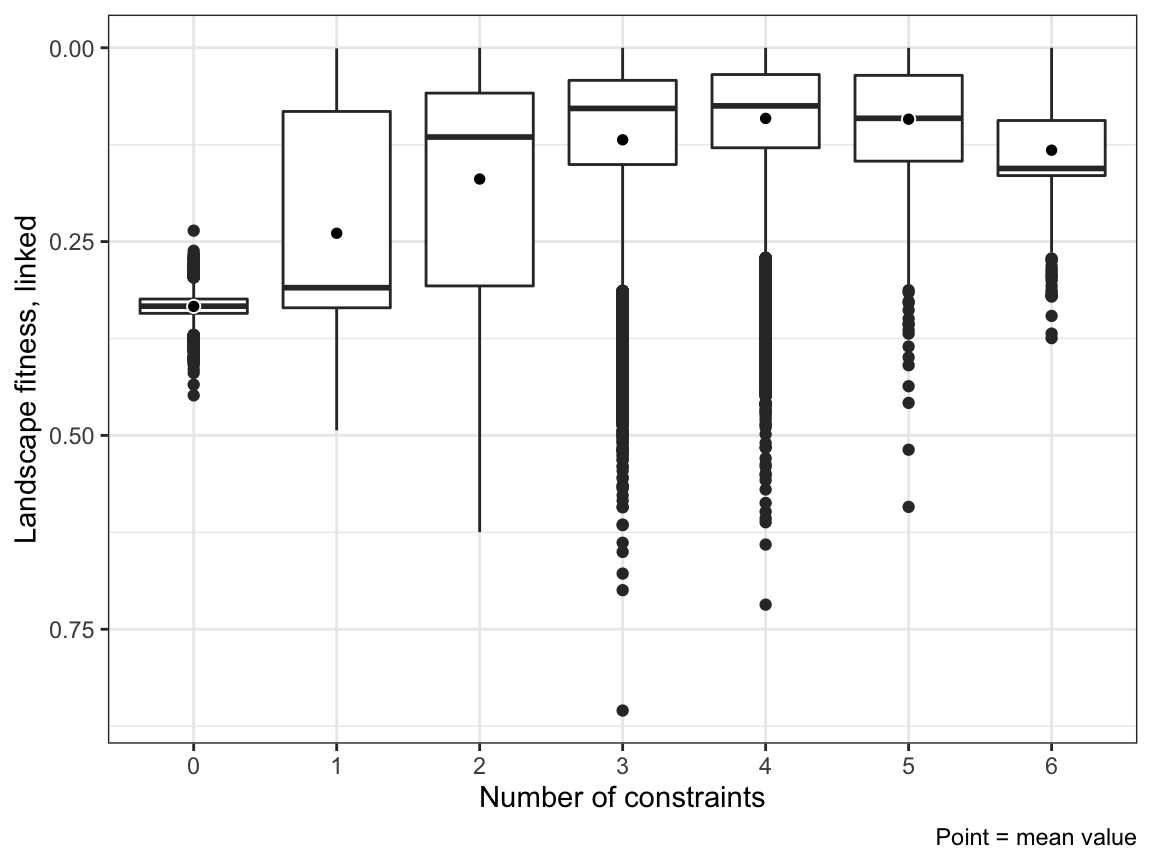
Boxplots

ggplot(sim_results, aes(x = n_constraints_f, y = landscape_fitness_linked)) +
  geom_boxplot() +
  stat_summary(geom = "point", fun.y = "mean",
               size = 2, pch = 21, fill = "black", color = "white") +
  scale_y_reverse() +
  labs(x = "Number of constraints",
       y = "Landscape fitness, linked",
       caption = "Point = mean value") +
  theme_bw()

## Warning: `fun.y` is deprecated. Use `fun` instead.

Constraint importance

Here we use a random forest to determine variable importance. We don’t need to include all the interactions (e.g. create_network + select + create_network * select, etc.) because random forests inherently pick those up.

# This takes a couple minutes to run
forest_model <- 
  randomForest(landscape_fitness_linked ~
                 create_network + select + disperse + 
                 compete + selectfor_d + catastrophe,
               data = sim_results)

According to Liz Dinsdale:

The mean decrease in Gini coefficient is a measure of how each variable contributes to the homogeneity of the nodes and leaves in the resulting random forest. Each time a particular variable is used to split a node, the Gini coefficient for the child nodes are calculated and compared to that of the original node. The Gini coefficient is a measure of homogeneity from 0 (homogeneous) to 1 (heterogeneous). The changes in Gini are summed for each variable and normalized at the end of the calculation. Variables that result in nodes with higher purity have a higher decrease in Gini coefficient.

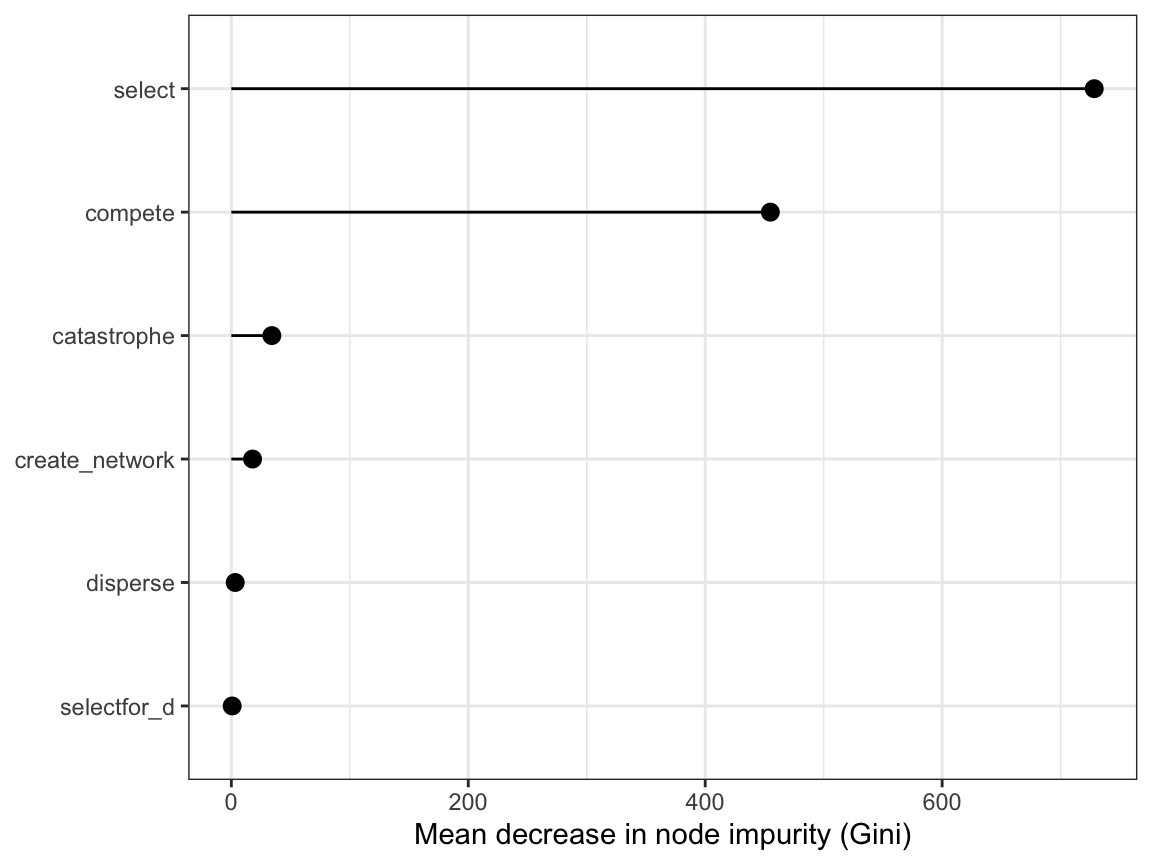
Basically, the higher the decrease in impurity, the more important the variable in explaining the outcome.

constraint_importance <- importance(forest_model) %>% 
  data.frame() %>% 
  rownames_to_column(var = "constraint") %>% 
  arrange(desc(IncNodePurity)) %>% 
  mutate(constraint = fct_inorder(constraint))

constraint_importance %>% 
  mutate(constraint = paste0("`", constraint, "`")) %>% 
  pandoc.table(justify = "lc")

constraint	IncNodePurity
select	728.4
compete	455
catastrophe	34.17
create_network	17.89
disperse	3.257
selectfor_d	0.699

ggplot(constraint_importance, 
       aes(x = IncNodePurity, y = fct_rev(constraint))) +
  geom_pointrangeh(aes(xmin = 0, xmax = IncNodePurity)) +
  labs(x = "Mean decrease in node impurity (Gini)",
       y = NULL) +
  theme_bw()

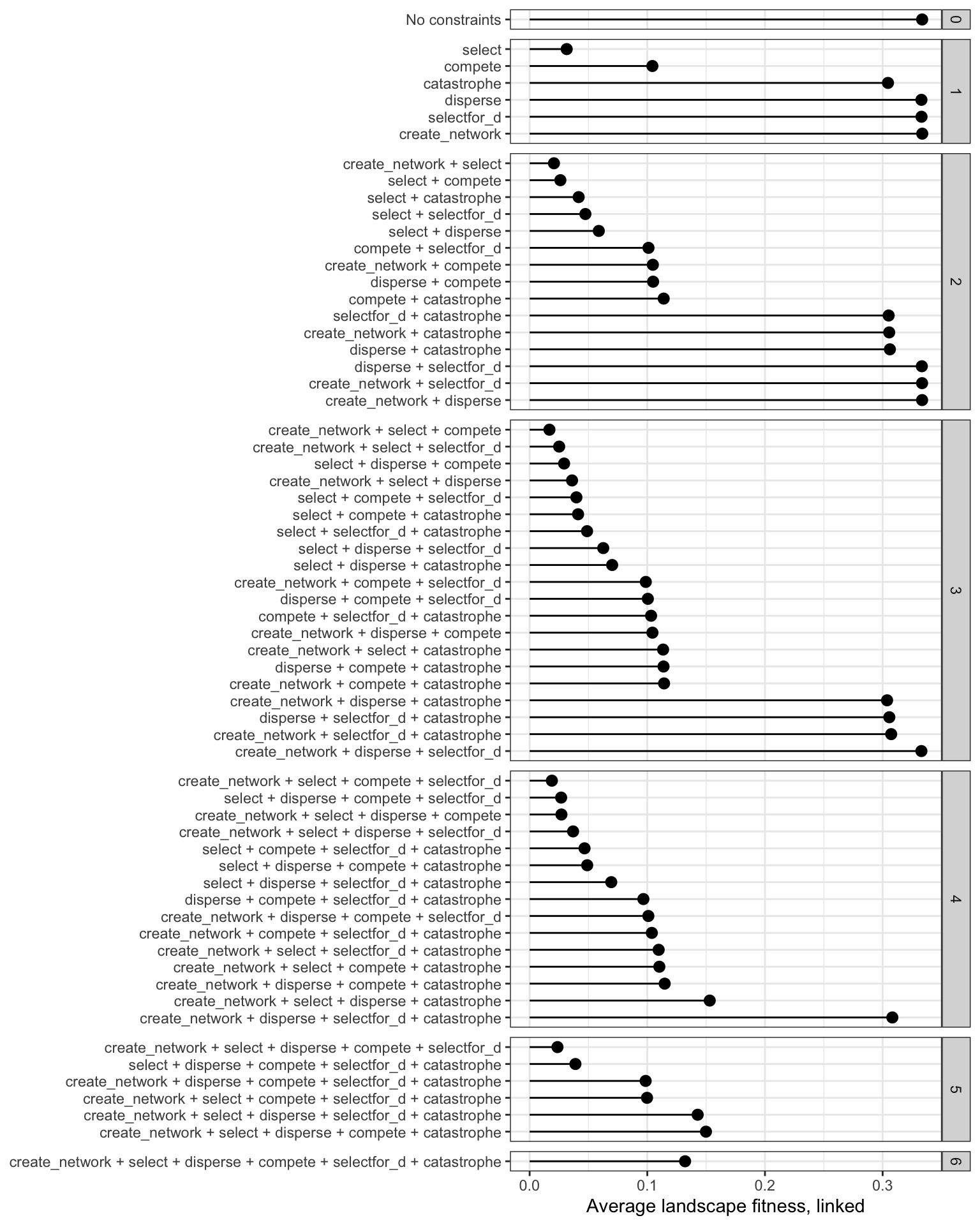
Power of different combinations of constraints

THIS IS MAGICAL.

# Create columns for every combination of constraint in the data (e.g. select &
# disperse, select & disperse & create_network) 
#
# By the inimitable Vincent Arel-Bundock
make_combinations <- function(df, m = 5) {
  com <- colnames(df)[2:ncol(df)] %>%
    combn(m) %>%
    as_tibble()
  out <- com %>%
    map(~ df[.]) %>%
    map(~ rowSums(.) == ncol(.)) %>%
    setNames(map(com, paste, collapse = " + ")) %>%
    as_tibble()
  return(out)
}

# Select just the run number and *_constraint TRUE/FALSE columns
constraint_combinations <- sim_results %>%
  select(runnum, ends_with("_constraint")) %>% 
  # Shrink names by removing "_constraint"
  rename_at(vars(ends_with("constraint")), 
            list(~str_replace_all(., "_constraint", "")))

# Find all combinations of variables (m = number of items in combination; m = 2
# means pairs, m = 3 means triplets, etc.)
all_constraint_combos <- map(2:6, ~make_combinations(constraint_combinations, m = .)) %>% 
  bind_cols(constraint_combinations, .)

# Select the outcome variables we care about (for now just
# landscape_fitness_linked) and join the constraint combinations
constraint_combo_outcomes <- sim_results %>%
  select(runnum, n_constraints, landscape_fitness_linked) %>% 
  right_join(all_constraint_combos, by = "runnum")

# Don't double count rows. If a row has two constraints like select and
# disperse, it'll also have select + disperse set to TRUE. If that's the case,
# we don't want to include it in just select or just disperse
constraint_combo_outcomes_nested <- constraint_combo_outcomes %>% 
  select(-n_constraints) %>% 
  # Make long
  gather(constraint_combo, value, -c(runnum, landscape_fitness_linked)) %>% 
  # Count how many constraints there are within each row based on + signs
  mutate(n = str_count(constraint_combo, "\\+") + 1) %>%
  # Only keep rows where the constraint is turned on
  filter(value == TRUE) %>%
  # Nest all the constraint combinations within each row
  group_by(runnum) %>% 
  nest()

# Only keep the values where n == max(n) for that row
constraint_combo_outcomes_filtered <- constraint_combo_outcomes_nested %>% 
  mutate(filtered = data %>% map(~filter(., n == max(.$n)))) %>% 
  select(-data) %>% 
  unnest(filtered)

# This omitted all the rows where n_constraints == 0, so add those back in
no_constraints <- constraint_combo_outcomes %>% 
  filter(n_constraints == 0) %>% 
  mutate(constraint_combo = "No constraints", n = 0) %>% 
  select(runnum, landscape_fitness_linked, constraint_combo, n)

constraint_combo_outcomes_done <- bind_rows(constraint_combo_outcomes_filtered,
                                            no_constraints) %>% 
  select(-value)

n_constraints_combos <- constraint_combo_outcomes_done %>%
  group_by(constraint_combo, n) %>%
  summarize(avg = mean(landscape_fitness_linked)) %>% 
  arrange(desc(n), desc(avg)) %>% 
  ungroup() %>% 
  mutate(constraint_combo = fct_inorder(constraint_combo))

ggplot(n_constraints_combos,
       aes(x = avg, y = constraint_combo)) +
  geom_pointrangeh(aes(xmin = 0, xmax = avg)) + 
  labs(x = "Average landscape fitness, linked",
       y = NULL) +
  facet_grid(rows = vars(n),
             scales = "free", space = "free") + 
  theme_bw()

Copyright © 2019–2020 Steven L. Peck and Andrew Heiss. Licensed under the MIT License. Code available on GitHub.