Compare distributions

library(tidyverse)
library(broom)
library(ggridges)
library(viridis)
library(flexmix)
library(pander)
library(here)

source(file.path(here(), "lib", "graphics.R"))

psm <- read_csv(file.path(here(), "data", "data_clean", "psm_clean.csv"))

psm_indexes_long <- psm %>%
  select(ID, starts_with("index")) %>%
  gather(index, value, -ID) %>%
  filter(!str_detect(index, "_z")) %>%
  mutate(index = fct_inorder(index, ordered = TRUE),
         index = fct_recode(index,
                            Perry = "index_perry",
                            MSPB5 = "index_msp",
                            Grant = "index_grant",
                            International = "index_intl"))

psm_indexes_long_z <- psm %>%
  select(ID, starts_with("index")) %>%
  gather(index, value, -ID) %>%
  filter(str_detect(index, "_z")) %>%
  mutate(index = fct_inorder(index, ordered = TRUE),
         index = fct_recode(index,
                            Perry = "index_perry_z",
                            MSPB5 = "index_msp_z",
                            Grant = "index_grant_z",
                            International = "index_intl_z"))

Raw index scores

ggplot(psm_indexes_long, aes(x = value, y = fct_rev(index), fill = index)) + 
  geom_density_ridges2(aes(height = ..density..),
                       stat = "density", size = 0.25) +
  scale_fill_viridis(discrete = TRUE, option = "viridis") +
  guides(fill = FALSE) +
  labs(x = "Index score", y = NULL) +
  theme_psm() + 
  theme(panel.grid.major.y = element_blank())

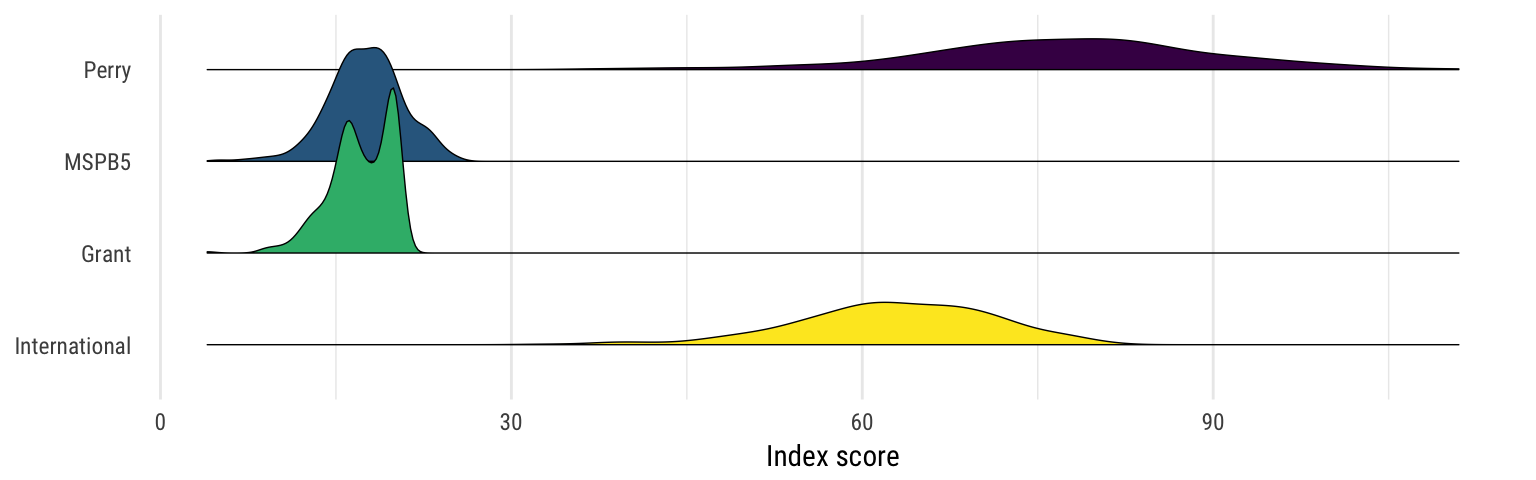
Standardized scores

ggplot(psm_indexes_long_z, aes(x = value, y = fct_rev(index), fill = index)) + 
  geom_density_ridges2(aes(height = ..density..),
                       stat = "density", size = 0.25) +
  scale_fill_viridis(discrete = TRUE, option = "viridis") +
  guides(fill = FALSE) +
  labs(x = "Standardized z-score", y = NULL) +
  theme_psm() + 
  theme(panel.grid.major.y = element_blank())

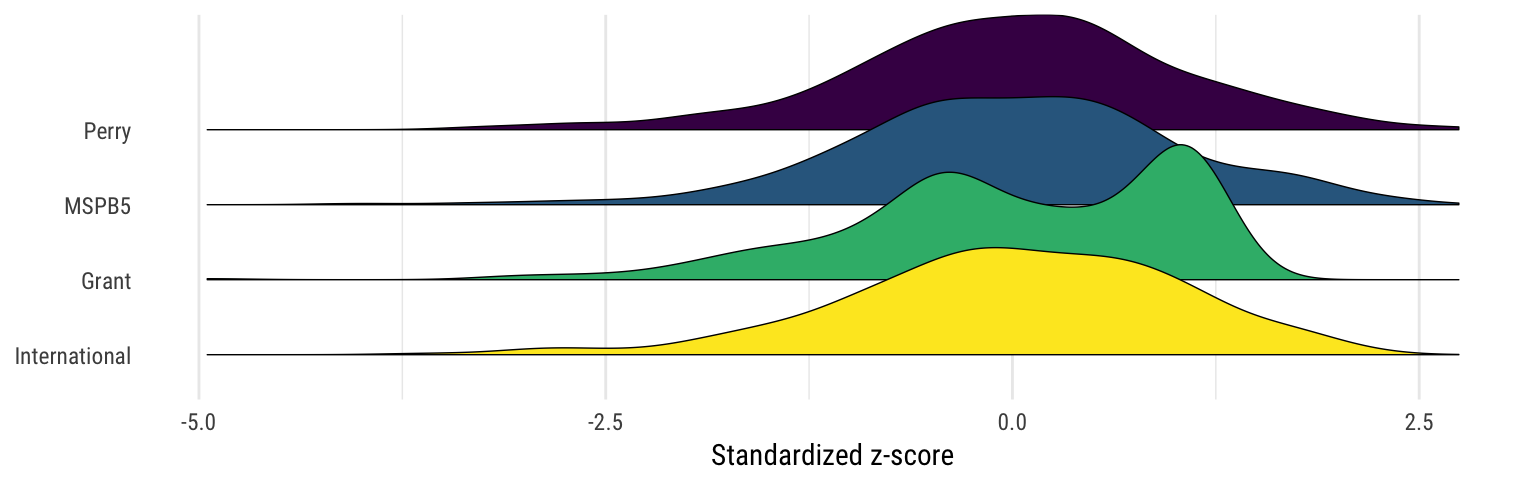
Or as a violin chart:

set.seed(1234)
ggplot(psm_indexes_long_z, aes(x = index, y = value, fill = index)) +
  geom_violin() +
  geom_point(position = "jitter", size = 0.5, alpha = 0.2) +
  stat_summary(fun.y = "mean", colour = "#eb6864", size = 4, geom = "point") +
  scale_fill_viridis(discrete = TRUE, option = "viridis") + 
  guides(fill = FALSE) +
  labs(x = NULL, y = "Standardized z-score") +
  theme_psm() +
  theme(panel.grid.major.x = element_blank())

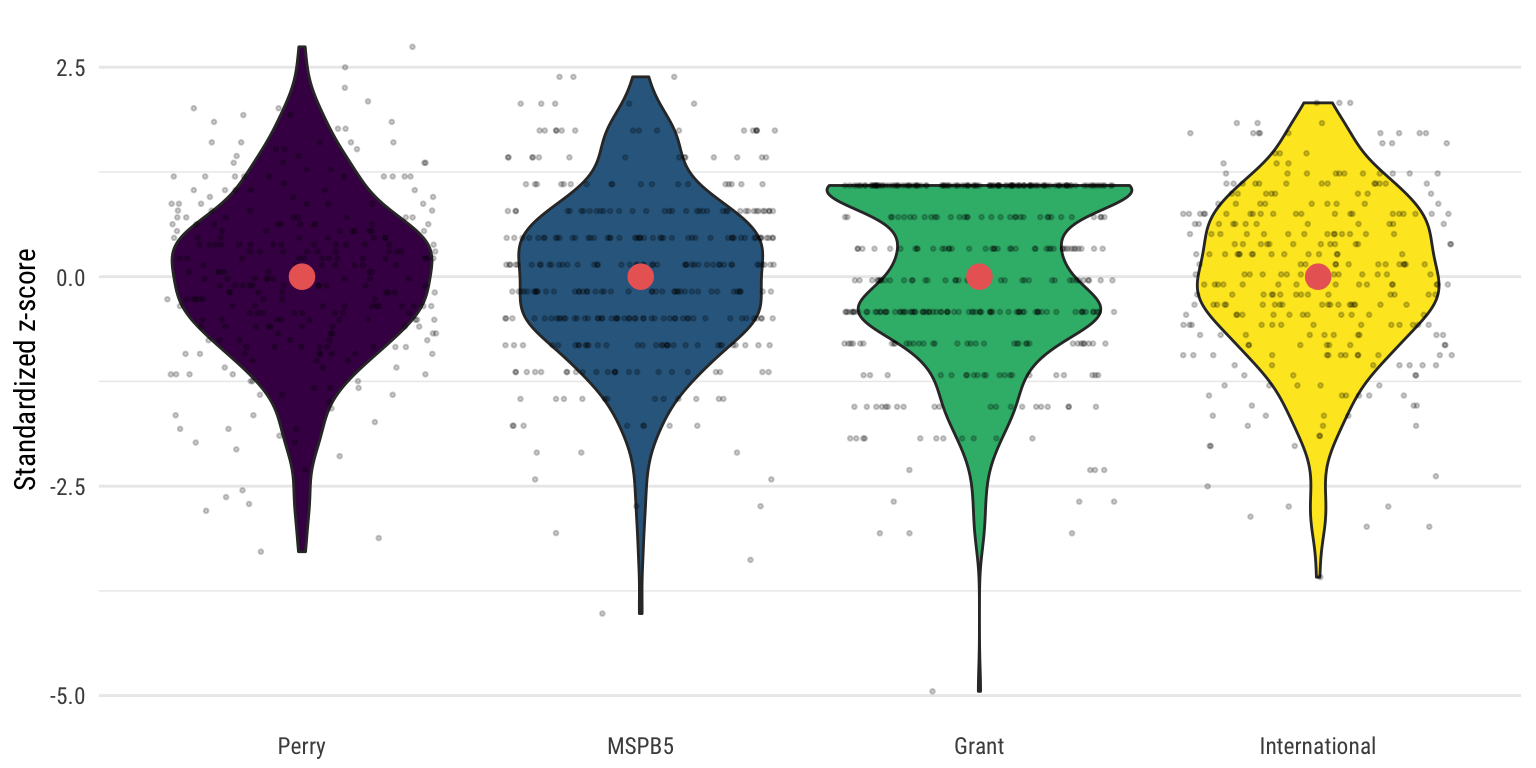
Check equality of distributions

psm_indexes <- psm %>%
  select(ID, starts_with("index")) 

# Null = distributions are the same
# If p is small, groups came from populations with different distributions
# https://www.graphpad.com/guides/prism/7/statistics/index.htm?interpreting_results_kolmogorov-smirnov_test.htm
ks_tests <- tribble(
  ~var1, ~var2, ~results,
  "Perry", "International", ks.test(psm_indexes$index_perry_z, psm_indexes$index_intl_z),
  "Perry", "Grant", ks.test(psm_indexes$index_perry_z, psm_indexes$index_grant_z),
  "Perry", "MSP85", ks.test(psm_indexes$index_perry_z, psm_indexes$index_msp_z),
  "MSP85", "International", ks.test(psm_indexes$index_msp_z, psm_indexes$index_intl_z),
  "MSP85", "Grant", ks.test(psm_indexes$index_msp_z, psm_indexes$index_grant_z),
  "Grant", "International", ks.test(psm_indexes$index_grant_z, psm_indexes$index_intl_z)
) %>%
  mutate(bloop = results %>% map(tidy)) %>%
  unnest(bloop)

ks_blanks <- data_frame(var1 = c("Perry", "MSP85", "Grant", "International")) %>%
  mutate(var2 = var1,
         statistic = 0)

star.labs <- c("***", "**", "*", "")
star.nums <- c("p < 0.001", "p < 0.01", "p < 0.05", "p > 0.05")

ks_long <- bind_rows(ks_tests, ks_blanks) %>%
  mutate_at(vars(var1, var2), funs(factor(., levels = ks_blanks$var1, ordered = TRUE))) %>%
  mutate(stars = as.character(symnum(p.value, 
                                     cutpoints = c(0, 0.001, 0.01, 0.05, 1),
                                     symbols = star.labs)),
         stars = ifelse(stars == "?", NA, stars),
         stars = factor(stars, levels = star.labs, ordered = TRUE),
         label = ifelse(!is.na(stars), paste(round(statistic, 2), stars), ""))

ggplot(ks_long, aes(x = fct_rev(var2), y = fct_rev(var1), fill = stars)) +
  geom_tile() +
  geom_text(aes(label = label),
            family = "Roboto Condensed", fontface = "plain") +
  scale_fill_manual(values = rev(c("#feedde", "#fdbe85", "#fd8d3c", "#d94701")),
                    breaks = star.labs, labels = star.nums, name = NULL,
                    drop = FALSE, na.value = "grey95") +
  labs(x = NULL, y = NULL, title = "Kolmogorov-Smirnov statistics",
       subtitle = "Pairwise comparison between standardized distributions") +
  coord_equal() +
  theme_psm() +
  theme(panel.grid.major = element_blank(),
        legend.position = "bottom")

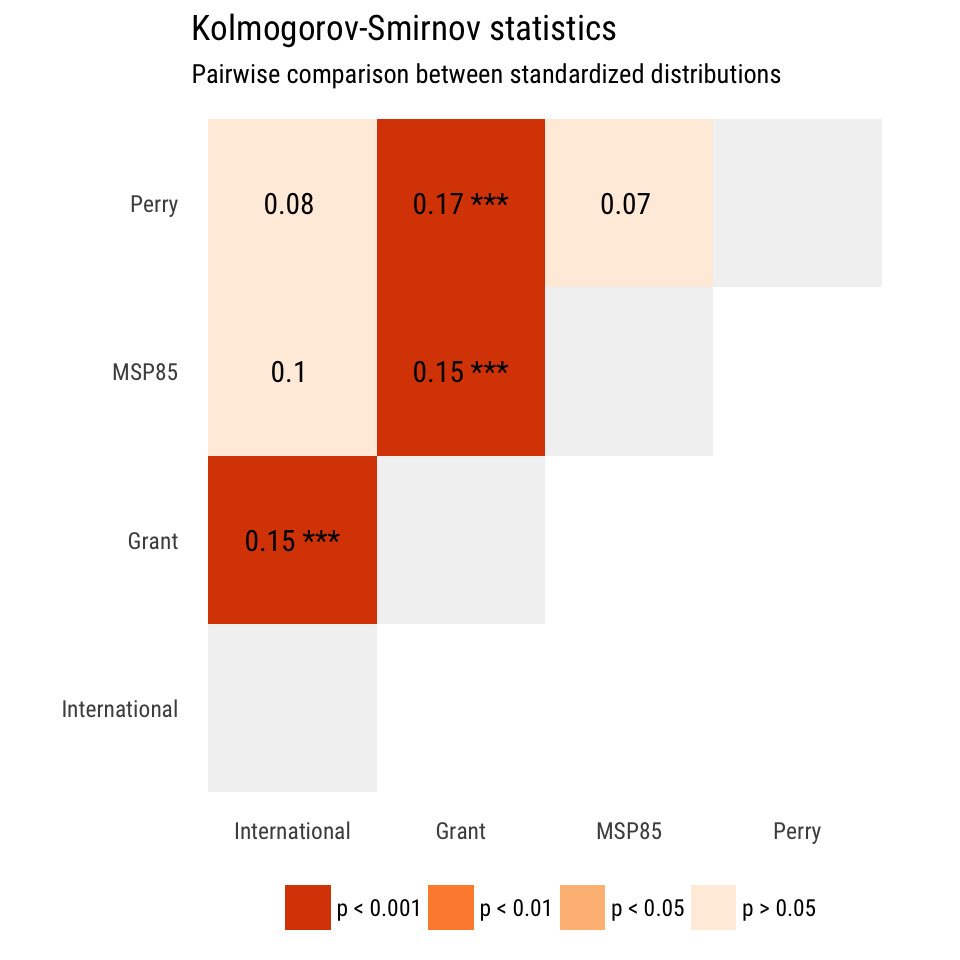
Grant is different from everything else; nothing else is different from each other.

Check divergence of distributions

Instead of hypothesis testing, we can see how much entropic divergence there is between different distributions. Kullback-Leibler (KL) divergence is particularly useful for comparing two probability distributions. This blog post is really helpful for getting the intuition behind KL divergence, and this post and this video (starting at 47:52) explain why it’s asymmetric and what that actually means. (Though good luck interpreting it in any non-information theoretic way).

Calculating the KL divergence statistic is surprisingly convoluted in R. There are a ton of different packages that do it (entropy, philentropy, flexmix, FNN, and laplacesdemons, to name a few), and they all have different syntaxes. Additionally, some are designed to deal with discrete random variables, not continuous random variables, so they require discretized vectors to work (like entropy: you have to run KL.empirical(discretize(x1, numBins = N), discretize(x2, numBins = N)), and numBins has a huge effect on the divergence if the vectors aren’t huge).

Fortunately, flexmix::KLdiv() works well with continuous random variables (it probably does some magic discretization behind the scenes?), and it will output a matrix of all pairwise comparisons if you feed it a matrix with multiple columns.

In general, the smaller the number, the less divergence there is. There’s no magic critical value—just that values closer to zero mean the distributions are more similar.

index_densities <- cbind(perry = density(psm_indexes$index_perry_z, na.rm = TRUE)$y, 
                         msp = density(psm_indexes$index_msp_z, na.rm = TRUE)$y,
                         grant = density(psm_indexes$index_grant_z, na.rm = TRUE)$y,
                         intl = density(psm_indexes$index_intl_z, na.rm = TRUE)$y)

round(flexmix::KLdiv(index_densities), 3) %>%
  pandoc.table()

	perry	msp	grant	intl
perry	0	0.136	1.176	0.13
msp	0.133	0	0.626	0.014
grant	1.478	0.812	0	0.763
intl	0.144	0.015	0.608	0

LS0tCnRpdGxlOiAiQ29tcGFyZSBkaXN0cmlidXRpb25zIgpkYXRlOiAiMjAxNy0xMi0yOSIKZWRpdG9yX29wdGlvbnM6IAogIGNodW5rX291dHB1dF90eXBlOiBjb25zb2xlCi0tLQoKYGBge3IgbG9hZC1saWJyYXJpZXMsIG1lc3NhZ2U9RkFMU0UsIHdhcm5pbmc9RkFMU0V9CmxpYnJhcnkodGlkeXZlcnNlKQpsaWJyYXJ5KGJyb29tKQpsaWJyYXJ5KGdncmlkZ2VzKQpsaWJyYXJ5KHZpcmlkaXMpCmxpYnJhcnkoZmxleG1peCkKbGlicmFyeShwYW5kZXIpCmxpYnJhcnkoaGVyZSkKCnNvdXJjZShmaWxlLnBhdGgoaGVyZSgpLCAibGliIiwgImdyYXBoaWNzLlIiKSkKCnBzbSA8LSByZWFkX2NzdihmaWxlLnBhdGgoaGVyZSgpLCAiZGF0YSIsICJkYXRhX2NsZWFuIiwgInBzbV9jbGVhbi5jc3YiKSkKCnBzbV9pbmRleGVzX2xvbmcgPC0gcHNtICU+JQogIHNlbGVjdChJRCwgc3RhcnRzX3dpdGgoImluZGV4IikpICU+JQogIGdhdGhlcihpbmRleCwgdmFsdWUsIC1JRCkgJT4lCiAgZmlsdGVyKCFzdHJfZGV0ZWN0KGluZGV4LCAiX3oiKSkgJT4lCiAgbXV0YXRlKGluZGV4ID0gZmN0X2lub3JkZXIoaW5kZXgsIG9yZGVyZWQgPSBUUlVFKSwKICAgICAgICAgaW5kZXggPSBmY3RfcmVjb2RlKGluZGV4LAogICAgICAgICAgICAgICAgICAgICAgICAgICAgUGVycnkgPSAiaW5kZXhfcGVycnkiLAogICAgICAgICAgICAgICAgICAgICAgICAgICAgTVNQQjUgPSAiaW5kZXhfbXNwIiwKICAgICAgICAgICAgICAgICAgICAgICAgICAgIEdyYW50ID0gImluZGV4X2dyYW50IiwKICAgICAgICAgICAgICAgICAgICAgICAgICAgIEludGVybmF0aW9uYWwgPSAiaW5kZXhfaW50bCIpKQoKcHNtX2luZGV4ZXNfbG9uZ196IDwtIHBzbSAlPiUKICBzZWxlY3QoSUQsIHN0YXJ0c193aXRoKCJpbmRleCIpKSAlPiUKICBnYXRoZXIoaW5kZXgsIHZhbHVlLCAtSUQpICU+JQogIGZpbHRlcihzdHJfZGV0ZWN0KGluZGV4LCAiX3oiKSkgJT4lCiAgbXV0YXRlKGluZGV4ID0gZmN0X2lub3JkZXIoaW5kZXgsIG9yZGVyZWQgPSBUUlVFKSwKICAgICAgICAgaW5kZXggPSBmY3RfcmVjb2RlKGluZGV4LAogICAgICAgICAgICAgICAgICAgICAgICAgICAgUGVycnkgPSAiaW5kZXhfcGVycnlfeiIsCiAgICAgICAgICAgICAgICAgICAgICAgICAgICBNU1BCNSA9ICJpbmRleF9tc3BfeiIsCiAgICAgICAgICAgICAgICAgICAgICAgICAgICBHcmFudCA9ICJpbmRleF9ncmFudF96IiwKICAgICAgICAgICAgICAgICAgICAgICAgICAgIEludGVybmF0aW9uYWwgPSAiaW5kZXhfaW50bF96IikpCmBgYAoKCiMjIFJhdyBpbmRleCBzY29yZXMKCmBgYHtyIHBsb3QtcmF3LXNjb3Jlcy1yaWRnZSwgZmlnLndpZHRoPTgsIGZpZy5oZWlnaHQ9Mi41LCB3YXJuaW5nPUZBTFNFfQpnZ3Bsb3QocHNtX2luZGV4ZXNfbG9uZywgYWVzKHggPSB2YWx1ZSwgeSA9IGZjdF9yZXYoaW5kZXgpLCBmaWxsID0gaW5kZXgpKSArIAogIGdlb21fZGVuc2l0eV9yaWRnZXMyKGFlcyhoZWlnaHQgPSAuLmRlbnNpdHkuLiksCiAgICAgICAgICAgICAgICAgICAgICAgc3RhdCA9ICJkZW5zaXR5Iiwgc2l6ZSA9IDAuMjUpICsKICBzY2FsZV9maWxsX3ZpcmlkaXMoZGlzY3JldGUgPSBUUlVFLCBvcHRpb24gPSAidmlyaWRpcyIpICsKICBndWlkZXMoZmlsbCA9IEZBTFNFKSArCiAgbGFicyh4ID0gIkluZGV4IHNjb3JlIiwgeSA9IE5VTEwpICsKICB0aGVtZV9wc20oKSArIAogIHRoZW1lKHBhbmVsLmdyaWQubWFqb3IueSA9IGVsZW1lbnRfYmxhbmsoKSkKYGBgCgoKIyMgU3RhbmRhcmRpemVkIHNjb3JlcwoKYGBge3IgcGxvdC1zdGQtc2NvcmVzLXJpZGdlLCBmaWcud2lkdGg9OCwgZmlnLmhlaWdodD0yLjUsIHdhcm5pbmc9RkFMU0V9CmdncGxvdChwc21faW5kZXhlc19sb25nX3osIGFlcyh4ID0gdmFsdWUsIHkgPSBmY3RfcmV2KGluZGV4KSwgZmlsbCA9IGluZGV4KSkgKyAKICBnZW9tX2RlbnNpdHlfcmlkZ2VzMihhZXMoaGVpZ2h0ID0gLi5kZW5zaXR5Li4pLAogICAgICAgICAgICAgICAgICAgICAgIHN0YXQgPSAiZGVuc2l0eSIsIHNpemUgPSAwLjI1KSArCiAgc2NhbGVfZmlsbF92aXJpZGlzKGRpc2NyZXRlID0gVFJVRSwgb3B0aW9uID0gInZpcmlkaXMiKSArCiAgZ3VpZGVzKGZpbGwgPSBGQUxTRSkgKwogIGxhYnMoeCA9ICJTdGFuZGFyZGl6ZWQgei1zY29yZSIsIHkgPSBOVUxMKSArCiAgdGhlbWVfcHNtKCkgKyAKICB0aGVtZShwYW5lbC5ncmlkLm1ham9yLnkgPSBlbGVtZW50X2JsYW5rKCkpCmBgYAoKT3IgYXMgYSB2aW9saW4gY2hhcnQ6CgpgYGB7ciBwbG90LXN0ZC1zY29yZXMtdmlvbGluLCBmaWcud2lkdGg9OCwgZmlnLmhlaWdodD00LCB3YXJuaW5nPUZBTFNFfQpzZXQuc2VlZCgxMjM0KQpnZ3Bsb3QocHNtX2luZGV4ZXNfbG9uZ196LCBhZXMoeCA9IGluZGV4LCB5ID0gdmFsdWUsIGZpbGwgPSBpbmRleCkpICsKICBnZW9tX3Zpb2xpbigpICsKICBnZW9tX3BvaW50KHBvc2l0aW9uID0gImppdHRlciIsIHNpemUgPSAwLjUsIGFscGhhID0gMC4yKSArCiAgc3RhdF9zdW1tYXJ5KGZ1bi55ID0gIm1lYW4iLCBjb2xvdXIgPSAiI2ViNjg2NCIsIHNpemUgPSA0LCBnZW9tID0gInBvaW50IikgKwogIHNjYWxlX2ZpbGxfdmlyaWRpcyhkaXNjcmV0ZSA9IFRSVUUsIG9wdGlvbiA9ICJ2aXJpZGlzIikgKyAKICBndWlkZXMoZmlsbCA9IEZBTFNFKSArCiAgbGFicyh4ID0gTlVMTCwgeSA9ICJTdGFuZGFyZGl6ZWQgei1zY29yZSIpICsKICB0aGVtZV9wc20oKSArCiAgdGhlbWUocGFuZWwuZ3JpZC5tYWpvci54ID0gZWxlbWVudF9ibGFuaygpKQpgYGAKCgojIyBDaGVjayBlcXVhbGl0eSBvZiBkaXN0cmlidXRpb25zCgpgYGB7ciBrcy1jYWxjdWxhdGlvbnMsIHdhcm5pbmc9RkFMU0UsIGZpZy53aWR0aD01LCBmaWcuaGVpZ2h0PTV9CnBzbV9pbmRleGVzIDwtIHBzbSAlPiUKICBzZWxlY3QoSUQsIHN0YXJ0c193aXRoKCJpbmRleCIpKSAKCiMgTnVsbCA9IGRpc3RyaWJ1dGlvbnMgYXJlIHRoZSBzYW1lCiMgSWYgcCBpcyBzbWFsbCwgZ3JvdXBzIGNhbWUgZnJvbSBwb3B1bGF0aW9ucyB3aXRoIGRpZmZlcmVudCBkaXN0cmlidXRpb25zCiMgaHR0cHM6Ly93d3cuZ3JhcGhwYWQuY29tL2d1aWRlcy9wcmlzbS83L3N0YXRpc3RpY3MvaW5kZXguaHRtP2ludGVycHJldGluZ19yZXN1bHRzX2tvbG1vZ29yb3Ytc21pcm5vdl90ZXN0Lmh0bQprc190ZXN0cyA8LSB0cmliYmxlKAogIH52YXIxLCB+dmFyMiwgfnJlc3VsdHMsCiAgIlBlcnJ5IiwgIkludGVybmF0aW9uYWwiLCBrcy50ZXN0KHBzbV9pbmRleGVzJGluZGV4X3BlcnJ5X3osIHBzbV9pbmRleGVzJGluZGV4X2ludGxfeiksCiAgIlBlcnJ5IiwgIkdyYW50Iiwga3MudGVzdChwc21faW5kZXhlcyRpbmRleF9wZXJyeV96LCBwc21faW5kZXhlcyRpbmRleF9ncmFudF96KSwKICAiUGVycnkiLCAiTVNQODUiLCBrcy50ZXN0KHBzbV9pbmRleGVzJGluZGV4X3BlcnJ5X3osIHBzbV9pbmRleGVzJGluZGV4X21zcF96KSwKICAiTVNQODUiLCAiSW50ZXJuYXRpb25hbCIsIGtzLnRlc3QocHNtX2luZGV4ZXMkaW5kZXhfbXNwX3osIHBzbV9pbmRleGVzJGluZGV4X2ludGxfeiksCiAgIk1TUDg1IiwgIkdyYW50Iiwga3MudGVzdChwc21faW5kZXhlcyRpbmRleF9tc3BfeiwgcHNtX2luZGV4ZXMkaW5kZXhfZ3JhbnRfeiksCiAgIkdyYW50IiwgIkludGVybmF0aW9uYWwiLCBrcy50ZXN0KHBzbV9pbmRleGVzJGluZGV4X2dyYW50X3osIHBzbV9pbmRleGVzJGluZGV4X2ludGxfeikKKSAlPiUKICBtdXRhdGUoYmxvb3AgPSByZXN1bHRzICU+JSBtYXAodGlkeSkpICU+JQogIHVubmVzdChibG9vcCkKCmtzX2JsYW5rcyA8LSBkYXRhX2ZyYW1lKHZhcjEgPSBjKCJQZXJyeSIsICJNU1A4NSIsICJHcmFudCIsICJJbnRlcm5hdGlvbmFsIikpICU+JQogIG11dGF0ZSh2YXIyID0gdmFyMSwKICAgICAgICAgc3RhdGlzdGljID0gMCkKCnN0YXIubGFicyA8LSBjKCIqKioiLCAiKioiLCAiKiIsICIiKQpzdGFyLm51bXMgPC0gYygicCA8IDAuMDAxIiwgInAgPCAwLjAxIiwgInAgPCAwLjA1IiwgInAgPiAwLjA1IikKCmtzX2xvbmcgPC0gYmluZF9yb3dzKGtzX3Rlc3RzLCBrc19ibGFua3MpICU+JQogIG11dGF0ZV9hdCh2YXJzKHZhcjEsIHZhcjIpLCBmdW5zKGZhY3RvciguLCBsZXZlbHMgPSBrc19ibGFua3MkdmFyMSwgb3JkZXJlZCA9IFRSVUUpKSkgJT4lCiAgbXV0YXRlKHN0YXJzID0gYXMuY2hhcmFjdGVyKHN5bW51bShwLnZhbHVlLCAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIGN1dHBvaW50cyA9IGMoMCwgMC4wMDEsIDAuMDEsIDAuMDUsIDEpLAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgc3ltYm9scyA9IHN0YXIubGFicykpLAogICAgICAgICBzdGFycyA9IGlmZWxzZShzdGFycyA9PSAiPyIsIE5BLCBzdGFycyksCiAgICAgICAgIHN0YXJzID0gZmFjdG9yKHN0YXJzLCBsZXZlbHMgPSBzdGFyLmxhYnMsIG9yZGVyZWQgPSBUUlVFKSwKICAgICAgICAgbGFiZWwgPSBpZmVsc2UoIWlzLm5hKHN0YXJzKSwgcGFzdGUocm91bmQoc3RhdGlzdGljLCAyKSwgc3RhcnMpLCAiIikpCgpnZ3Bsb3Qoa3NfbG9uZywgYWVzKHggPSBmY3RfcmV2KHZhcjIpLCB5ID0gZmN0X3Jldih2YXIxKSwgZmlsbCA9IHN0YXJzKSkgKwogIGdlb21fdGlsZSgpICsKICBnZW9tX3RleHQoYWVzKGxhYmVsID0gbGFiZWwpLAogICAgICAgICAgICBmYW1pbHkgPSAiUm9ib3RvIENvbmRlbnNlZCIsIGZvbnRmYWNlID0gInBsYWluIikgKwogIHNjYWxlX2ZpbGxfbWFudWFsKHZhbHVlcyA9IHJldihjKCIjZmVlZGRlIiwgIiNmZGJlODUiLCAiI2ZkOGQzYyIsICIjZDk0NzAxIikpLAogICAgICAgICAgICAgICAgICAgIGJyZWFrcyA9IHN0YXIubGFicywgbGFiZWxzID0gc3Rhci5udW1zLCBuYW1lID0gTlVMTCwKICAgICAgICAgICAgICAgICAgICBkcm9wID0gRkFMU0UsIG5hLnZhbHVlID0gImdyZXk5NSIpICsKICBsYWJzKHggPSBOVUxMLCB5ID0gTlVMTCwgdGl0bGUgPSAiS29sbW9nb3Jvdi1TbWlybm92IHN0YXRpc3RpY3MiLAogICAgICAgc3VidGl0bGUgPSAiUGFpcndpc2UgY29tcGFyaXNvbiBiZXR3ZWVuIHN0YW5kYXJkaXplZCBkaXN0cmlidXRpb25zIikgKwogIGNvb3JkX2VxdWFsKCkgKwogIHRoZW1lX3BzbSgpICsKICB0aGVtZShwYW5lbC5ncmlkLm1ham9yID0gZWxlbWVudF9ibGFuaygpLAogICAgICAgIGxlZ2VuZC5wb3NpdGlvbiA9ICJib3R0b20iKQpgYGAKCkdyYW50IGlzIGRpZmZlcmVudCBmcm9tIGV2ZXJ5dGhpbmcgZWxzZTsgbm90aGluZyBlbHNlIGlzIGRpZmZlcmVudCBmcm9tIGVhY2ggb3RoZXIuCgoKIyMgQ2hlY2sgZGl2ZXJnZW5jZSBvZiBkaXN0cmlidXRpb25zCgpJbnN0ZWFkIG9mIGh5cG90aGVzaXMgdGVzdGluZywgd2UgY2FuIHNlZSBob3cgbXVjaCBlbnRyb3BpYyBkaXZlcmdlbmNlIHRoZXJlIGlzIGJldHdlZW4gZGlmZmVyZW50IGRpc3RyaWJ1dGlvbnMuIEt1bGxiYWNrLUxlaWJsZXIgKEtMKSBkaXZlcmdlbmNlIGlzIHBhcnRpY3VsYXJseSB1c2VmdWwgZm9yIGNvbXBhcmluZyB0d28gcHJvYmFiaWxpdHkgZGlzdHJpYnV0aW9ucy4gW1RoaXMgYmxvZyBwb3N0XShodHRwczovL3d3dy5jb3VudGJheWVzaWUuY29tL2Jsb2cvMjAxNy81Lzkva3VsbGJhY2stbGVpYmxlci1kaXZlcmdlbmNlLWV4cGxhaW5lZCkgaXMgcmVhbGx5IGhlbHBmdWwgZm9yIGdldHRpbmcgdGhlIGludHVpdGlvbiBiZWhpbmQgS0wgZGl2ZXJnZW5jZSwgYW5kIFt0aGlzIHBvc3RdKGh0dHBzOi8vd3d3LmpvaG5kY29vay5jb20vYmxvZy8yMDE3LzExLzA4L3doeS1pcy1rdWxsYmFjay1sZWlibGVyLWRpdmVyZ2VuY2Utbm90LWEtZGlzdGFuY2UvKSBhbmQgW3RoaXMgdmlkZW9dKGh0dHBzOi8veW91dHUuYmUvQlNHei1OUnpsNzQ/dD00N201MHMpIChzdGFydGluZyBhdCA0Nzo1MikgZXhwbGFpbiB3aHkgaXQncyBhc3ltbWV0cmljIGFuZCB3aGF0IHRoYXQgYWN0dWFsbHkgbWVhbnMuIChbVGhvdWdoIGdvb2QgbHVjayBpbnRlcnByZXRpbmcgaXQgaW4gYW55IG5vbi1pbmZvcm1hdGlvbiB0aGVvcmV0aWMgd2F5XShodHRwczovL3N0YXRzLnN0YWNrZXhjaGFuZ2UuY29tL3F1ZXN0aW9ucy8xMTE0NDUvYW5hbHlzaXMtb2Yta3VsbGJhY2stbGVpYmxlci1kaXZlcmdlbmNlKSkuCgpDYWxjdWxhdGluZyB0aGUgS0wgZGl2ZXJnZW5jZSBzdGF0aXN0aWMgaXMgc3VycHJpc2luZ2x5IGNvbnZvbHV0ZWQgaW4gUi4gVGhlcmUgYXJlIGEgdG9uIG9mIGRpZmZlcmVudCBwYWNrYWdlcyB0aGF0IGRvIGl0IChgZW50cm9weWAsIGBwaGlsZW50cm9weWAsIGBmbGV4bWl4YCwgYEZOTmAsIGFuZCBgbGFwbGFjZXNkZW1vbnNgLCB0byBuYW1lIGEgZmV3KSwgYW5kIHRoZXkgYWxsIGhhdmUgZGlmZmVyZW50IHN5bnRheGVzLiBBZGRpdGlvbmFsbHksIHNvbWUgYXJlIGRlc2lnbmVkIHRvIGRlYWwgd2l0aCBkaXNjcmV0ZSByYW5kb20gdmFyaWFibGVzLCBub3QgY29udGludW91cyByYW5kb20gdmFyaWFibGVzLCBzbyB0aGV5IHJlcXVpcmUgZGlzY3JldGl6ZWQgdmVjdG9ycyB0byB3b3JrIChsaWtlIGBlbnRyb3B5YDogeW91IGhhdmUgdG8gcnVuIGBLTC5lbXBpcmljYWwoZGlzY3JldGl6ZSh4MSwgbnVtQmlucyA9IE4pLCBkaXNjcmV0aXplKHgyLCBudW1CaW5zID0gTikpYCwgYW5kIGBudW1CaW5zYCBoYXMgYSBodWdlIGVmZmVjdCBvbiB0aGUgZGl2ZXJnZW5jZSBpZiB0aGUgdmVjdG9ycyBhcmVuJ3QgaHVnZSkuIAoKRm9ydHVuYXRlbHksIGBmbGV4bWl4OjpLTGRpdigpYCB3b3JrcyB3ZWxsIHdpdGggY29udGludW91cyByYW5kb20gdmFyaWFibGVzIChpdCBwcm9iYWJseSBkb2VzIHNvbWUgbWFnaWMgZGlzY3JldGl6YXRpb24gYmVoaW5kIHRoZSBzY2VuZXM/KSwgKmFuZCogaXQgd2lsbCBvdXRwdXQgYSBtYXRyaXggb2YgYWxsIHBhaXJ3aXNlIGNvbXBhcmlzb25zIGlmIHlvdSBmZWVkIGl0IGEgbWF0cml4IHdpdGggbXVsdGlwbGUgY29sdW1ucy4KCkluIGdlbmVyYWwsIHRoZSBzbWFsbGVyIHRoZSBudW1iZXIsIHRoZSBsZXNzIGRpdmVyZ2VuY2UgdGhlcmUgaXMuIFRoZXJlJ3Mgbm8gbWFnaWMgY3JpdGljYWwgdmFsdWXigJRqdXN0IHRoYXQgdmFsdWVzIGNsb3NlciB0byB6ZXJvIG1lYW4gdGhlIGRpc3RyaWJ1dGlvbnMgYXJlIG1vcmUgc2ltaWxhci4KCmBgYHtyIGtsLWNhbGN1bGF0aW9ucywgcmVzdWx0cz0iYXNpcyJ9CmluZGV4X2RlbnNpdGllcyA8LSBjYmluZChwZXJyeSA9IGRlbnNpdHkocHNtX2luZGV4ZXMkaW5kZXhfcGVycnlfeiwgbmEucm0gPSBUUlVFKSR5LCAKICAgICAgICAgICAgICAgICAgICAgICAgIG1zcCA9IGRlbnNpdHkocHNtX2luZGV4ZXMkaW5kZXhfbXNwX3osIG5hLnJtID0gVFJVRSkkeSwKICAgICAgICAgICAgICAgICAgICAgICAgIGdyYW50ID0gZGVuc2l0eShwc21faW5kZXhlcyRpbmRleF9ncmFudF96LCBuYS5ybSA9IFRSVUUpJHksCiAgICAgICAgICAgICAgICAgICAgICAgICBpbnRsID0gZGVuc2l0eShwc21faW5kZXhlcyRpbmRleF9pbnRsX3osIG5hLnJtID0gVFJVRSkkeSkKCnJvdW5kKGZsZXhtaXg6OktMZGl2KGluZGV4X2RlbnNpdGllcyksIDMpICU+JQogIHBhbmRvYy50YWJsZSgpCmBgYAo=

Compare distributions

2017-12-29

Raw index scores

Standardized scores

Check equality of distributions

Check divergence of distributions