Replicate original tables
Before doing fancier analysis and visualizations, I replicated the three summary tables that were originally created with SPSS.
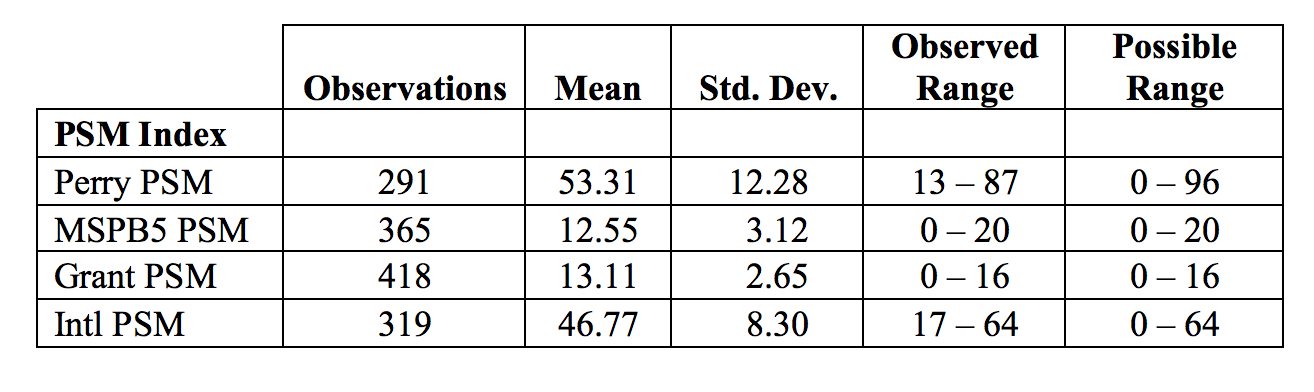
Table 1: Summary statistics
Original table
Table 1: Summary statistics
Table using current data
psm_indexes_long <- psm %>%
select (ID, starts_with ("index" )) %>% gather (index, value, - ID) %>% filter (! str_detect (index, "_z" )) %>% mutate (index = fct_inorder (index, ordered = TRUE ), index = fct_recode (index,
Perry = "index_perry" ,
MSPB5 = "index_msp" ,
Grant = "index_grant" ,
International = "index_intl" ))
psm_indexes_long %>%
filter (! is.na (value)) %>% group_by (index) %>% summarize (Observations = n (), Mean = mean (value),
` Std. Dev ` = sd (value),
Minimum = min (value),
Maximum = max (value)) %>%
rename (Index = index) %>% pandoc.table (justify = "lccccc" )
Perry
291
77.31
12.28
37
111
MSPB5
365
17.55
3.122
5
25
Grant
418
17.11
2.65
4
20
International
319
62.77
8.302
33
80
Uh oh, this doesn’t match. 🤔
The mean, min, and max are all off, but oddly enough, the N and standard deviations are both correct.
Table 2: High PSM
Original table
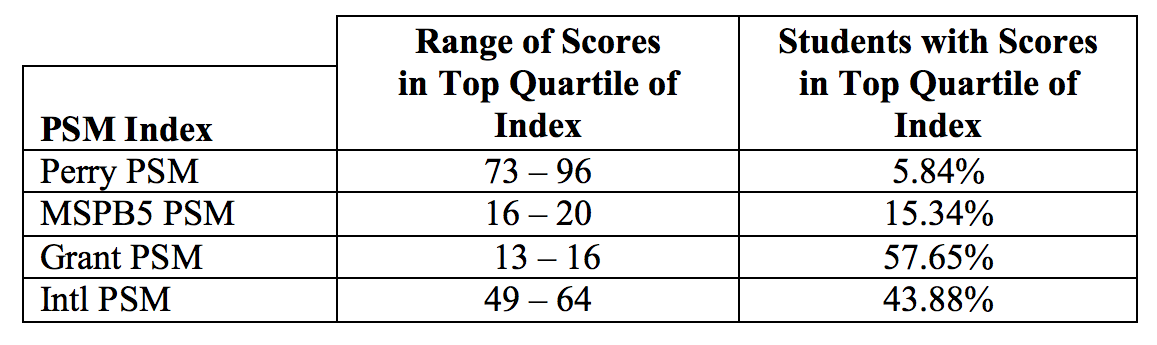
Table 2: Proportions of Students with “High” Levels of PSM
Table using current data
This is slightly tricky (and wrong) because the ranges of possible values don’t match what’s in the original Word file. The Perry index, for example, should range from 0–96, but in reality it goes up to a maximum of 111 (and I don’t know what the actual real life maximum should be, given what it’s calculating). The same issue appears in the other indexes. Grant should range from 0–16, but here it ranges from 0–20, so the top quartile is 15–20 instead of 13–16.
So for now this is wrong, but the code exists and everything can be made right once we figure out the issues with index calculation.
possible_quantiles <- psm_indexes_long %>%
distinct (index) %>% mutate (possible_min = c (0 , 0 , 0 , 0 ), possible_max = c (116 , 25 , 20 , 80 )) %>%
nest (- index) %>% mutate (quantiles = data %>% map (~ quantile (.$ possible_min: .$ possible_max))) %>% unnest (quantiles %>% map (tidy))possible_quantiles_wide <- possible_quantiles %>%
mutate (names = fct_inorder (names)) %>% spread (names, x) %>% mutate (` Top quartile range ` = paste0 (` 75% ` , "-" , ` 100% ` ), ` Possible range (wrong?) ` = paste0 (` 0% ` , "-" , ` 100% ` ))
psm_index_quantiles <- psm_indexes_long %>%
filter (! is.na (value)) %>% nest (- index) %>% mutate (temp = map2 ( .x = data, .y = index,
~ mutate (.x, quartile = cut (
value,
breaks = filter (possible_quantiles, index == .y) %>% pull (x),
labels = FALSE , right = FALSE , include.lowest = TRUE
))
)) %>%
unnest (temp)psm_index_quantiles %>%
group_by (index, quartile) %>% summarize (n = n ()) %>% mutate (perc = n / sum (n)) %>% ungroup () %>% filter (quartile == 4 ) %>% left_join (possible_quantiles_wide, by = "index" ) %>% mutate (perc = scales:: percent (perc)) %>% select (Index = index, N = n, ` Possible range (wrong?) ` , ` Top quartile range ` , ` Students in top quartile ` = perc) %>%
pandoc.table (justify = "lcccc" , split.table = Inf )
Perry
59
0-116
87-116
20.3%
MSPB5
142
0-25
18.75-25
38.9%
Grant
355
0-20
15-20
84.9%
International
218
0-80
60-80
68.3%
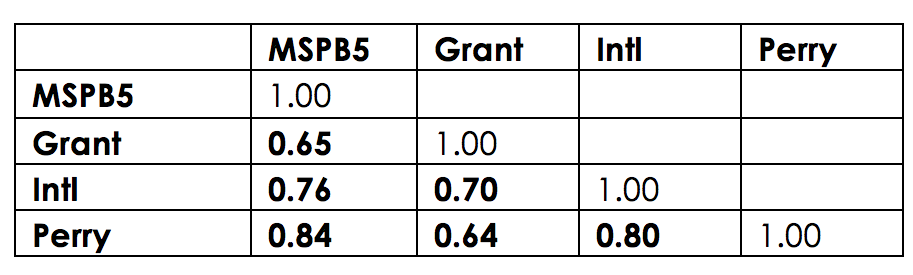
Table 3: PSM correlations
Original table
Table 3: Correlation Matrix for PSM Measures
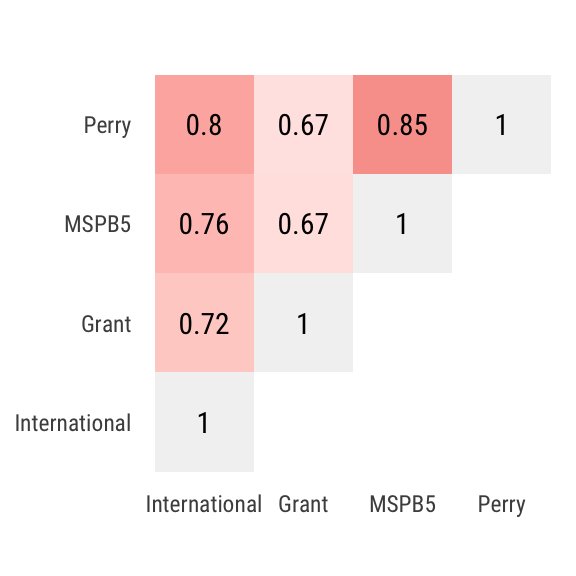
Table using current data
psm_cor <- psm_indexes_long %>%
spread (index, value) %>% select (- ID) %>% cor (use = "na.or.complete" )psm_cor[upper.tri (psm_cor)] <- NA
psm_cor_long <- psm_cor %>%
as.data.frame () %>% rownames_to_column () %>% as.tibble () %>% gather (var2, value, - rowname, na.rm = TRUE ) %>% mutate (rowname = fct_inorder (rowname, ordered = TRUE ), var2 = factor (var2, levels = levels (rowname), ordered= TRUE ))
ggplot (psm_cor_long, aes (x = fct_rev (rowname), y = fct_rev (var2), fill = value)) + geom_tile () + geom_text (aes (label = round (value, 2 )), family = "Roboto Condensed" , fontface = "plain" ) +
scale_fill_gradient (low = "white" , high = "#eb6864" , limit = c (floor (min (psm_cor_long$ value) * 10 ) / 10 , 0.999 ),
na.value = "grey95" ) +
labs (x = NULL , y = NULL ) + guides (fill = FALSE ) + coord_equal () + theme_psm () + theme (panel.grid.major = element_blank ())
LS0tCnRpdGxlOiAiU3VtbWFyeSBzdGF0aXN0aWNzIgpkYXRlOiAiMjAxNy0xMi0yOSIKZWRpdG9yX29wdGlvbnM6IAogIGNodW5rX291dHB1dF90eXBlOiBjb25zb2xlCi0tLQoKYGBge3IgbG9hZC1saWJyYXJpZXMsIG1lc3NhZ2U9RkFMU0UsIHdhcm5pbmc9RkFMU0V9CmxpYnJhcnkodGlkeXZlcnNlKQpsaWJyYXJ5KGJyb29tKQpsaWJyYXJ5KHBhbmRlcikKbGlicmFyeShnZ3JpZGdlcykKbGlicmFyeSh2aXJpZGlzKQpsaWJyYXJ5KGhlcmUpCgpzb3VyY2UoZmlsZS5wYXRoKGhlcmUoKSwgImxpYiIsICJncmFwaGljcy5SIikpCgpwc20gPC0gcmVhZF9jc3YoZmlsZS5wYXRoKGhlcmUoKSwgImRhdGEiLCAiZGF0YV9jbGVhbiIsICJwc21fY2xlYW4uY3N2IikpCmBgYAoKIyMgUmVwbGljYXRlIG9yaWdpbmFsIHRhYmxlcwoKQmVmb3JlIGRvaW5nIGZhbmNpZXIgYW5hbHlzaXMgYW5kIHZpc3VhbGl6YXRpb25zLCBJIHJlcGxpY2F0ZWQgdGhlIHRocmVlIHN1bW1hcnkgdGFibGVzIHRoYXQgd2VyZSBvcmlnaW5hbGx5IGNyZWF0ZWQgd2l0aCBTUFNTLgoKIyMjIFRhYmxlIDE6IFN1bW1hcnkgc3RhdGlzdGljcwoKIyMjIyBPcmlnaW5hbCB0YWJsZQoKPGRpdiBjbGFzcz0icm93Ij4KPGRpdiBjbGFzcz0iY29sLXNtLTEyIGNvbC1tZC04IGNvbC1tZC1vZmZzZXQtMiI+CgohW1RhYmxlIDE6IFN1bW1hcnkgc3RhdGlzdGljc10oaW1nL3RibDEucG5nKQoKPC9kaXY+CjwvZGl2PgoKIyMjIyBUYWJsZSB1c2luZyBjdXJyZW50IGRhdGEKCmBgYHtyIHBzbS1pbmRleC1zdW1tYXJ5LCByZXN1bHRzPSJhc2lzIn0KcHNtX2luZGV4ZXNfbG9uZyA8LSBwc20gJT4lCiAgc2VsZWN0KElELCBzdGFydHNfd2l0aCgiaW5kZXgiKSkgJT4lCiAgZ2F0aGVyKGluZGV4LCB2YWx1ZSwgLUlEKSAlPiUKICBmaWx0ZXIoIXN0cl9kZXRlY3QoaW5kZXgsICJfeiIpKSAlPiUKICBtdXRhdGUoaW5kZXggPSBmY3RfaW5vcmRlcihpbmRleCwgb3JkZXJlZCA9IFRSVUUpLAogICAgICAgICBpbmRleCA9IGZjdF9yZWNvZGUoaW5kZXgsCiAgICAgICAgICAgICAgICAgICAgICAgICAgICBQZXJyeSA9ICJpbmRleF9wZXJyeSIsCiAgICAgICAgICAgICAgICAgICAgICAgICAgICBNU1BCNSA9ICJpbmRleF9tc3AiLAogICAgICAgICAgICAgICAgICAgICAgICAgICAgR3JhbnQgPSAiaW5kZXhfZ3JhbnQiLAogICAgICAgICAgICAgICAgICAgICAgICAgICAgSW50ZXJuYXRpb25hbCA9ICJpbmRleF9pbnRsIikpCgpwc21faW5kZXhlc19sb25nICU+JQogIGZpbHRlcighaXMubmEodmFsdWUpKSAlPiUKICBncm91cF9ieShpbmRleCkgJT4lCiAgc3VtbWFyaXplKE9ic2VydmF0aW9ucyA9IG4oKSwKICAgICAgICAgICAgTWVhbiA9IG1lYW4odmFsdWUpLAogICAgICAgICAgICBgU3RkLiBEZXZgID0gc2QodmFsdWUpLAogICAgICAgICAgICBNaW5pbXVtID0gbWluKHZhbHVlKSwKICAgICAgICAgICAgTWF4aW11bSA9IG1heCh2YWx1ZSkpICU+JQogIHJlbmFtZShJbmRleCA9IGluZGV4KSAlPiUKICBwYW5kb2MudGFibGUoanVzdGlmeSA9ICJsY2NjY2MiKQpgYGAKCipVaCBvaCwgdGhpcyBkb2Vzbid0IG1hdGNoLiogYHIgZW1vOjpqaSgidGhpbmtpbmciKWAgCgpUaGUgbWVhbiwgbWluLCBhbmQgbWF4IGFyZSBhbGwgb2ZmLCBidXQgb2RkbHkgZW5vdWdoLCB0aGUgTiBhbmQgc3RhbmRhcmQgZGV2aWF0aW9ucyBhcmUgYm90aCBjb3JyZWN0LiAKCiMjIyBUYWJsZSAyOiBIaWdoIFBTTQoKIyMjIyBPcmlnaW5hbCB0YWJsZQoKPGRpdiBjbGFzcz0icm93Ij4KPGRpdiBjbGFzcz0iY29sLXNtLTEyIGNvbC1tZC04IGNvbC1tZC1vZmZzZXQtMiI+CgohW1RhYmxlIDI6IFByb3BvcnRpb25zIG9mIFN0dWRlbnRzIHdpdGggIkhpZ2giIExldmVscyBvZiBQU01dKGltZy90YmwyLnBuZykKCjwvZGl2Pgo8L2Rpdj4KCiMjIyMgVGFibGUgdXNpbmcgY3VycmVudCBkYXRhCgpUaGlzIGlzIHNsaWdodGx5IHRyaWNreSAoYW5kIHdyb25nKSBiZWNhdXNlIHRoZSByYW5nZXMgb2YgcG9zc2libGUgdmFsdWVzIGRvbid0IG1hdGNoIHdoYXQncyBpbiB0aGUgb3JpZ2luYWwgV29yZCBmaWxlLiBUaGUgUGVycnkgaW5kZXgsIGZvciBleGFtcGxlLCBzaG91bGQgcmFuZ2UgZnJvbSAw4oCTOTYsIGJ1dCBpbiByZWFsaXR5IGl0IGdvZXMgdXAgdG8gYSBtYXhpbXVtIG9mIDExMSAoYW5kIEkgZG9uJ3Qga25vdyB3aGF0IHRoZSBhY3R1YWwgcmVhbCBsaWZlIG1heGltdW0gc2hvdWxkIGJlLCBnaXZlbiB3aGF0IGl0J3MgY2FsY3VsYXRpbmcpLiBUaGUgc2FtZSBpc3N1ZSBhcHBlYXJzIGluIHRoZSBvdGhlciBpbmRleGVzLiBHcmFudCBzaG91bGQgcmFuZ2UgZnJvbSAw4oCTMTYsIGJ1dCBoZXJlIGl0IHJhbmdlcyBmcm9tIDDigJMyMCwgc28gdGhlIHRvcCBxdWFydGlsZSBpcyAxNeKAkzIwIGluc3RlYWQgb2YgMTPigJMxNi4KClNvIGZvciBub3cgdGhpcyBpcyB3cm9uZywgYnV0IHRoZSBjb2RlIGV4aXN0cyBhbmQgZXZlcnl0aGluZyBjYW4gYmUgbWFkZSByaWdodCBvbmNlIHdlIGZpZ3VyZSBvdXQgdGhlIGlzc3VlcyB3aXRoIGluZGV4IGNhbGN1bGF0aW9uLgoKYGBge3IgaW5kZXgtcXVhcnRpbGVzLCByZXN1bHRzPSJhc2lzIn0KcG9zc2libGVfcXVhbnRpbGVzIDwtIHBzbV9pbmRleGVzX2xvbmcgJT4lCiAgZGlzdGluY3QoaW5kZXgpICU+JQogIG11dGF0ZShwb3NzaWJsZV9taW4gPSBjKDAsIDAsIDAsIDApLAogICAgICAgICBwb3NzaWJsZV9tYXggPSBjKDExNiwgMjUsIDIwLCA4MCkpICU+JQogIG5lc3QoLWluZGV4KSAlPiUKICBtdXRhdGUocXVhbnRpbGVzID0gZGF0YSAlPiUgbWFwKH4gcXVhbnRpbGUoLiRwb3NzaWJsZV9taW46LiRwb3NzaWJsZV9tYXgpKSkgJT4lCiAgdW5uZXN0KHF1YW50aWxlcyAlPiUgbWFwKHRpZHkpKQoKcG9zc2libGVfcXVhbnRpbGVzX3dpZGUgPC0gcG9zc2libGVfcXVhbnRpbGVzICU+JSAKICBtdXRhdGUobmFtZXMgPSBmY3RfaW5vcmRlcihuYW1lcykpICU+JSAKICBzcHJlYWQobmFtZXMsIHgpICU+JQogIG11dGF0ZShgVG9wIHF1YXJ0aWxlIHJhbmdlYCA9IHBhc3RlMChgNzUlYCwgIi0iLCBgMTAwJWApLAogICAgICAgICBgUG9zc2libGUgcmFuZ2UgKHdyb25nPylgID0gcGFzdGUwKGAwJWAsICItIiwgYDEwMCVgKSkKCnBzbV9pbmRleF9xdWFudGlsZXMgPC0gcHNtX2luZGV4ZXNfbG9uZyAlPiUKICBmaWx0ZXIoIWlzLm5hKHZhbHVlKSkgJT4lCiAgbmVzdCgtaW5kZXgpICU+JQogIG11dGF0ZSh0ZW1wID0gbWFwMigKICAgIC54ID0gZGF0YSwgLnkgPSBpbmRleCwKICAgIH4gbXV0YXRlKC54LCBxdWFydGlsZSA9IGN1dCgKICAgICAgdmFsdWUsCiAgICAgIGJyZWFrcyA9IGZpbHRlcihwb3NzaWJsZV9xdWFudGlsZXMsIGluZGV4ID09IC55KSAlPiUgcHVsbCh4KSwKICAgICAgbGFiZWxzID0gRkFMU0UsIHJpZ2h0ID0gRkFMU0UsIGluY2x1ZGUubG93ZXN0ID0gVFJVRQogICAgKSkKICApKSAlPiUKICB1bm5lc3QodGVtcCkKCnBzbV9pbmRleF9xdWFudGlsZXMgJT4lCiAgZ3JvdXBfYnkoaW5kZXgsIHF1YXJ0aWxlKSAlPiUKICBzdW1tYXJpemUobiA9IG4oKSkgJT4lCiAgbXV0YXRlKHBlcmMgPSBuIC8gc3VtKG4pKSAlPiUKICB1bmdyb3VwKCkgJT4lCiAgZmlsdGVyKHF1YXJ0aWxlID09IDQpICU+JQogIGxlZnRfam9pbihwb3NzaWJsZV9xdWFudGlsZXNfd2lkZSwgYnkgPSAiaW5kZXgiKSAlPiUKICBtdXRhdGUocGVyYyA9IHNjYWxlczo6cGVyY2VudChwZXJjKSkgJT4lCiAgc2VsZWN0KEluZGV4ID0gaW5kZXgsIE4gPSBuLCBgUG9zc2libGUgcmFuZ2UgKHdyb25nPylgLAogICAgICAgICBgVG9wIHF1YXJ0aWxlIHJhbmdlYCwgYFN0dWRlbnRzIGluIHRvcCBxdWFydGlsZWAgPSBwZXJjKSAlPiUKICBwYW5kb2MudGFibGUoanVzdGlmeSA9ICJsY2NjYyIsIHNwbGl0LnRhYmxlID0gSW5mKQpgYGAKCgojIyMgVGFibGUgMzogUFNNIGNvcnJlbGF0aW9ucwoKIyMjIyBPcmlnaW5hbCB0YWJsZQoKPGRpdiBjbGFzcz0icm93Ij4KPGRpdiBjbGFzcz0iY29sLXNtLTEyIGNvbC1tZC04IGNvbC1tZC1vZmZzZXQtMiI+CgohW1RhYmxlIDM6IENvcnJlbGF0aW9uIE1hdHJpeCBmb3IgUFNNIE1lYXN1cmVzXShpbWcvdGJsMy5wbmcpCgo8L2Rpdj4KPC9kaXY+CgojIyMjIFRhYmxlIHVzaW5nIGN1cnJlbnQgZGF0YQoKYGBge3IgaW5kZXgtY29ycmVsYXRpb25zLCBmaWcud2lkdGg9MywgZmlnLmhlaWdodD0zfQpwc21fY29yIDwtIHBzbV9pbmRleGVzX2xvbmcgJT4lCiAgc3ByZWFkKGluZGV4LCB2YWx1ZSkgJT4lIAogIHNlbGVjdCgtSUQpICU+JSAKICBjb3IodXNlID0gIm5hLm9yLmNvbXBsZXRlIikKCnBzbV9jb3JbdXBwZXIudHJpKHBzbV9jb3IpXSA8LSBOQQoKcHNtX2Nvcl9sb25nIDwtIHBzbV9jb3IgJT4lCiAgYXMuZGF0YS5mcmFtZSgpICU+JQogIHJvd25hbWVzX3RvX2NvbHVtbigpICU+JQogIGFzLnRpYmJsZSgpICU+JQogIGdhdGhlcih2YXIyLCB2YWx1ZSwgLXJvd25hbWUsIG5hLnJtID0gVFJVRSkgJT4lCiAgbXV0YXRlKHJvd25hbWUgPSBmY3RfaW5vcmRlcihyb3duYW1lLCBvcmRlcmVkID0gVFJVRSksCiAgICAgICAgIHZhcjIgPSBmYWN0b3IodmFyMiwgbGV2ZWxzID0gbGV2ZWxzKHJvd25hbWUpLCBvcmRlcmVkPVRSVUUpKQoKZ2dwbG90KHBzbV9jb3JfbG9uZywgYWVzKHggPSBmY3RfcmV2KHJvd25hbWUpLCB5ID0gZmN0X3Jldih2YXIyKSwgZmlsbCA9IHZhbHVlKSkgKwogIGdlb21fdGlsZSgpICsKICBnZW9tX3RleHQoYWVzKGxhYmVsID0gcm91bmQodmFsdWUsIDIpKSwKICAgICAgICAgICAgZmFtaWx5ID0gIlJvYm90byBDb25kZW5zZWQiLCBmb250ZmFjZSA9ICJwbGFpbiIpICsKICBzY2FsZV9maWxsX2dyYWRpZW50KGxvdyA9ICJ3aGl0ZSIsIGhpZ2ggPSAiI2ViNjg2NCIsIAogICAgICAgICAgICAgICAgICAgICAgbGltaXQgPSBjKGZsb29yKG1pbihwc21fY29yX2xvbmckdmFsdWUpICogMTApIC8gMTAsIDAuOTk5KSwKICAgICAgICAgICAgICAgICAgICAgIG5hLnZhbHVlID0gImdyZXk5NSIpICsKICBsYWJzKHggPSBOVUxMLCB5ID0gTlVMTCkgKwogIGd1aWRlcyhmaWxsID0gRkFMU0UpICsKICBjb29yZF9lcXVhbCgpICsKICB0aGVtZV9wc20oKSArCiAgdGhlbWUocGFuZWwuZ3JpZC5tYWpvciA9IGVsZW1lbnRfYmxhbmsoKSkKYGBgCg==