Modeling susceptibility
Meredith Conroy and Andrew Heiss
February 21, 2018
knitr::opts_chunk$set(cache = FALSE, fig.retina = 2,
tidy.opts = list(width.cutoff = 120), # For code
width = 120) # For outputlibrary(tidyverse)
library(broom)
library(ggstance)
library(patchwork)
library(pander)
library(stargazer)
library(here)
source(file.path(here(), "lib", "pander_options.R"))
source(file.path(here(), "lib", "graphics.R"))
source(file.path(here(), "lib", "labels.R"))
stargazer2word <- FALSE
# By default, R uses polynomial contrasts for ordered factors in linear models
# options("contrasts")
# So make ordered factors use treatment contrasts instead
options(contrasts = rep("contr.treatment", 2))
# Or do it on a single variable:
# contrasts(df$x) <- "contr.treatment"
survey_clean <- readRDS(file.path(here(), "Data", "survey_clean.rds"))# Create a new formula based on a given DV and IVs (specified as a formulaa)
build_formula <- function(DV, IVs) {
reformulate(attr(terms(IVs), "term.labels"), response = DV)
}
get_stargazer_labs <- function(model) {
coefs <- tidy(model) %>%
left_join(coef.names, by = c("term" = "coef.name")) %>%
distinct(term, coef.clean) %>%
mutate(coef.clean = as.character(coef.clean))
return(coefs$coef.clean)
}
get_mode <- function(x) {
names(which.max(table(x)))
}
predict_values <- function(model, model_name) {
# Calculate the means of all five personality traits based on the data used in
# the given model
personality_means <- model$model %>%
summarise_at(vars(OPENNESS, CONSCIENTIOUSNESS, EXTRAVERSION,
AGREEABLENESS, NEUROTICISM), mean)
# Row of 1s
personality_1 <- data_frame(personality = colnames(personality_means),
value = 1) %>%
spread(personality, value)
# Row of 0s
personality_0 <- data_frame(personality = colnames(personality_means),
value = 0) %>%
spread(personality, value)
# Data frame of possible personality values (mean, 0, and 1)
personality_possibilities <- bind_rows(personality_means,
personality_0, personality_1)
# All combinations of mean, 0, and 1 personality values
new_data_personalities <- expand.grid(personality_possibilities) %>%
mutate(id = row_number()) %>%
gather(key, value, -id) %>%
group_by(id) %>%
filter(sum(value == 0) == 1 & !any(value == 1) |
sum(value == 1) == 1 & !any(value == 0)) %>%
spread(key, value) %>%
mutate(index = 1) %>%
ungroup() %>%
select(-id)
# Mean or modal values for all other model IVs
control_means <- data_frame(index = 1, frame = 0:1,
sex_rev = get_mode(survey_clean$sex),
race_rev = get_mode(survey_clean$race),
age_cat = get_mode(survey_clean$age_cat),
democrat_rev = get_mode(survey_clean$democrat),
republican_rev = get_mode(survey_clean$republican),
POLITICAL_KNOWLEDGE = mean(model$model$POLITICAL_KNOWLEDGE),
NC = mean(model$model$NC))
# Add mean/modal values to each possible personality combination
new_data_full <- new_data_personalities %>%
left_join(control_means, by = "index") %>%
select(-index)
frame_labs <- case_when(
model_name == model_kkk_name ~ frame_labs_kkk_guns_plot,
model_name == model_guns_name ~ frame_labs_kkk_guns_plot,
model_name == model_stemcells_name ~ frame_labs_stemcells_plot,
model_name == model_af_ac_name ~ frame_labs_aa_plot
)
# Finally use new data in model to generate predicted values
plot_predict <- augment(model, newdata = new_data_full) %>%
gather(key, value, one_of(colnames(personality_means))) %>%
left_join(coef.names, by = c("key" = "coef.name")) %>%
filter(value %in% c(0, 1)) %>%
mutate(value = factor(value, levels = c(0, 1),
labels = c("Low (0) ", "High (1)"),
ordered = TRUE),
frame = factor(frame, levels = c(0, 1),
labels = frame_labs, ordered = TRUE),
coef.clean = fct_inorder(coef.clean),
model_name = model_name)
return(plot_predict)
}Susceptibility to issue frames
# Base model (sans DV, since that gets added later)
indep_vars <- ~
# Main controls
sex_rev + race_rev + age_cat + democrat_rev + republican_rev +
# Frame
frame +
# Personality
OPENNESS * frame +
CONSCIENTIOUSNESS * frame +
EXTRAVERSION * frame +
AGREEABLENESS * frame +
NEUROTICISM * frame +
# Other traits
POLITICAL_KNOWLEDGE * frame +
NC * frame
# KKK
df_kkk <- survey_clean %>%
rename(frame = KKKFrame_CivLibs)
model_kkk <- lm(build_formula("KKK_Support", indep_vars),
data = df_kkk, weights = weight)
# Guns
df_guns <- survey_clean %>%
rename(frame = GunFrame_CivLibs)
model_guns <- lm(build_formula("Gun_Support", indep_vars),
data = df_guns, weights = weight)
# Stem cell research
df_stemcells <- survey_clean %>%
rename(frame = StemCellsFrame_Positive)
model_stemcells <- lm(build_formula("StemCellsSupport", indep_vars),
data = df_stemcells, weights = weight)
# Affirmative action
df_af_ac <- survey_clean %>%
rename(frame = AAFrame_positive)
model_af_ac <- lm(build_formula("AASupport", indep_vars),
data = df_af_ac, weights = weight)
models <- tribble(
~model, ~model_name,
model_kkk, model_kkk_name,
model_guns, model_guns_name,
model_stemcells, model_stemcells_name,
model_af_ac, model_af_ac_name
) %>%
mutate(model_name = fct_inorder(model_name, ordered = TRUE))models_tidy <- models %>%
mutate(tidy_model = model %>% map(~ tidy(., conf.int = TRUE)))
coefs_to_plot <- c("OPENNESS", "CONSCIENTIOUSNESS", "EXTRAVERSION",
"AGREEABLENESS", "NEUROTICISM", "POLITICAL_KNOWLEDGE", "NC",
"frame:OPENNESS", "frame:CONSCIENTIOUSNESS",
"frame:EXTRAVERSION", "frame:AGREEABLENESS",
"frame:NEUROTICISM", "frame:POLITICAL_KNOWLEDGE", "frame:NC")
df_coef_plot <- models_tidy %>%
unnest(tidy_model) %>%
mutate(low = estimate - std.error,
high = estimate + std.error) %>%
left_join(coef.names, by = c("term" = "coef.name")) %>%
filter(term != "(Intercept)") %>%
mutate(coef.clean = fct_rev(fct_inorder(coef.clean, ordered = TRUE)),
model_name = fct_rev(model_name)) %>%
mutate(facet = case_when(
term %in% coefs_to_plot & str_detect(term, ":") ~ "Frame ×\npersonality",
term %in% coefs_to_plot & !str_detect(term, ":") ~ "Personality",
TRUE ~ "Controls"
)) %>%
mutate(facet = factor(facet,
levels = c("Personality", "Frame ×\npersonality", "Controls"),
ordered = TRUE))
coef_plot <- ggplot(df_coef_plot, aes(x = estimate, y = coef.clean, colour = model_name)) +
geom_vline(xintercept = 0, colour = "black") +
geom_pointrangeh(aes(xmin = low, xmax = high), size = 0.25,
position = position_dodgev(0.5)) +
scale_colour_manual(values = framing.palette("palette.color")[5:1]) +
guides(color = guide_legend(title = NULL, nrow = 1, byrow = TRUE, reverse = TRUE)) +
labs(x = "Coefficient", y = NULL) +
theme_framing() + theme(legend.position = "bottom") +
facet_wrap(~ facet, scales = "free")
coef_plot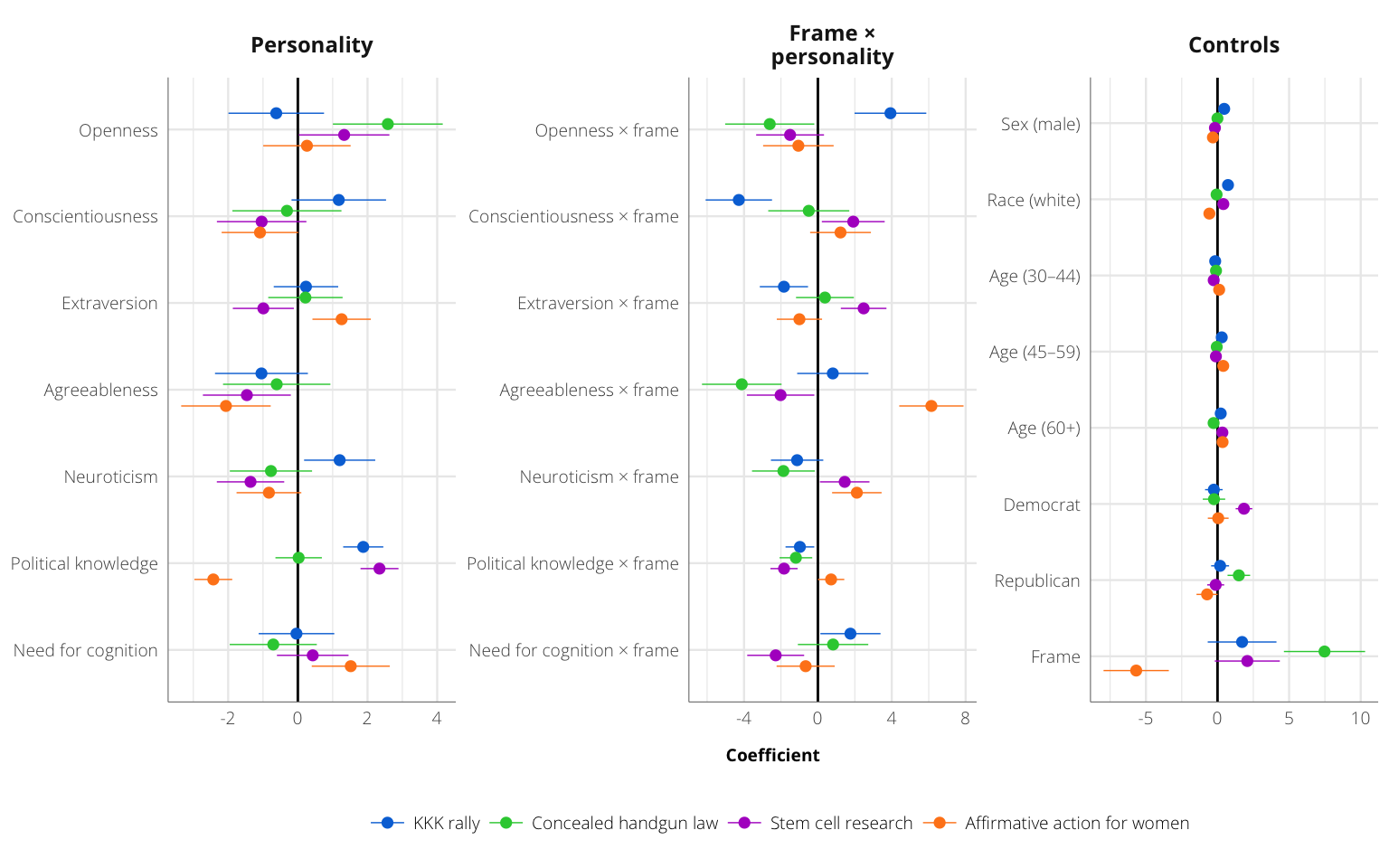
caption <- c("Coefficients for all four issue models")
save.fig.caption(coef_plot, filename = "coef_plot",
width = 8, height = 5, caption = caption)title <- "Susceptibility to issue frames"
out.file <- file.path(here(), "Output", "table_model_results.html")
stargazer(model_kkk, model_guns, model_stemcells, model_af_ac,
type = "html", digits = 2, intercept.bottom = FALSE,
title = title, out = out.file,
report = "vc*s", dep.var.caption = "",
dep.var.labels = c(model_kkk_name, model_guns_name, model_stemcells_name,
str_replace(model_af_ac_name_plot, "\\n", "<br>")),
covariate.labels = get_stargazer_labs(model_kkk))| KKK rally | Concealed handgun law | Stem cell research |
Affirmative action for women |
|
| (1) | (2) | (3) | (4) | |
| Intercept | 0.11 | 2.75 | 3.73** | 6.93*** |
| (1.76) | (2.04) | (1.66) | (1.76) | |
| Sex (male) | 0.47** | -0.01 | -0.18 | -0.32* |
| (0.21) | (0.24) | (0.20) | (0.19) | |
| Race (white) | 0.73*** | -0.07 | 0.41* | -0.57*** |
| (0.22) | (0.27) | (0.21) | (0.21) | |
| Age (30–44) | -0.16 | -0.11 | -0.27 | 0.12 |
| (0.30) | (0.34) | (0.28) | (0.28) | |
| Age (45–59) | 0.30 | -0.05 | -0.11 | 0.40 |
| (0.29) | (0.32) | (0.28) | (0.27) | |
| Age (60+) | 0.22 | -0.27 | 0.34 | 0.35 |
| (0.30) | (0.35) | (0.28) | (0.29) | |
| Democrat | -0.26 | -0.25 | 1.85*** | 0.05 |
| (0.61) | (0.78) | (0.58) | (0.73) | |
| Republican | 0.18 | 1.49* | -0.13 | -0.73 |
| (0.63) | (0.79) | (0.59) | (0.74) | |
| Frame | 1.72 | 7.47*** | 2.08 | -5.68** |
| (2.40) | (2.84) | (2.27) | (2.28) | |
| Openness | -0.62 | 2.58 | 1.33 | 0.26 |
| (1.37) | (1.58) | (1.30) | (1.25) | |
| Conscientiousness | 1.18 | -0.31 | -1.04 | -1.09 |
| (1.36) | (1.57) | (1.28) | (1.10) | |
| Extraversion | 0.23 | 0.22 | -0.99 | 1.26 |
| (0.93) | (1.07) | (0.88) | (0.84) | |
| Agreeableness | -1.04 | -0.61 | -1.46 | -2.06 |
| (1.33) | (1.54) | (1.26) | (1.29) | |
| Neuroticism | 1.20 | -0.77 | -1.36 | -0.83 |
| (1.02) | (1.18) | (0.97) | (0.93) | |
| Political knowledge | 1.88*** | 0.02 | 2.34*** | -2.43*** |
| (0.58) | (0.67) | (0.55) | (0.54) | |
| Need for cognition | -0.04 | -0.71 | 0.43 | 1.52 |
| (1.09) | (1.25) | (1.03) | (1.12) | |
| Openness × frame | 3.93** | -2.61 | -1.51 | -1.06 |
| (1.94) | (2.41) | (1.84) | (1.91) | |
| Conscientiousness × frame | -4.28** | -0.49 | 1.92 | 1.22 |
| (1.80) | (2.19) | (1.70) | (1.65) | |
| Extraversion × frame | -1.84 | 0.38 | 2.48** | -1.00 |
| (1.31) | (1.57) | (1.24) | (1.23) | |
| Agreeableness × frame | 0.81 | -4.12* | -2.02 | 6.15*** |
| (1.93) | (2.16) | (1.83) | (1.74) | |
| Neuroticism × frame | -1.13 | -1.87 | 1.45 | 2.11 |
| (1.42) | (1.70) | (1.34) | (1.34) | |
| Political knowledge × frame | -0.97 | -1.19 | -1.83** | 0.71 |
| (0.78) | (0.88) | (0.74) | (0.71) | |
| Need for cognition × frame | 1.76 | 0.82 | -2.29 | -0.66 |
| (1.63) | (1.91) | (1.54) | (1.57) | |
| Observations | 392 | 401 | 393 | 393 |
| R2 | 0.24 | 0.19 | 0.32 | 0.25 |
| Adjusted R2 | 0.20 | 0.15 | 0.27 | 0.20 |
| Residual Std. Error | 1.90 (df = 369) | 2.19 (df = 378) | 1.80 (df = 370) | 1.73 (df = 370) |
| F Statistic | 5.38*** (df = 22; 369) | 4.12*** (df = 22; 378) | 7.74*** (df = 22; 370) | 5.53*** (df = 22; 370) |
| Note: | p<0.1; p<0.05; p<0.01 | |||
Predicted means
plot_labs <- tribble(
~model_name, ~add_legend, ~add_ylab, ~first,
model_kkk_name, FALSE, FALSE, TRUE,
model_guns_name, FALSE, FALSE, FALSE,
model_stemcells_name, FALSE, TRUE, FALSE,
model_af_ac_name, TRUE, FALSE, FALSE
) %>%
mutate(model_name_char = model_name,
model_name = fct_inorder(model_name, ordered = TRUE))
plot_predicted <- function(df, model_name, add_legend, add_ylab, first) {
p <- ggplot(df, aes(x = frame, y = .fitted, color = value)) +
geom_pointrange(aes(ymin = .fitted + (qnorm(0.025) * .se.fit),
ymax = .fitted + (qnorm(0.975) * .se.fit)),
position = position_dodge(width = 0.5),
size = 1, fatten = 1) +
labs(x = NULL, y = NULL, title = model_name) +
guides(color = guide_legend(title = "Trait score",
override.aes = list(size = 0.4))) +
scale_colour_manual(values = framing.palette("palette.bw2"), name = NULL) +
scale_y_continuous(breaks = c(1, 3, 5, 7)) +
coord_cartesian(ylim = c(0, 9)) +
theme_framing() + theme(panel.grid.minor = element_blank(),
panel.grid.major.x = element_blank(),
strip.text = element_text(size = rel(0.8)),
plot.title = element_text(size = rel(1.1)),
axis.text = element_text(size = rel(0.7))) +
facet_wrap(~ coef.clean, nrow = 1)
if (!add_legend) {
p <- p + guides(color = FALSE)
}
if (add_ylab) {
p <- p + labs(y = "Average predicted support")
}
if (!first) {
p <- p + theme(plot.title = element_text(margin = margin(t = 20, b = 3)))
}
p
}
models_predicted <- models %>%
left_join(plot_labs, by = "model_name") %>%
mutate(predicted = map2(.x = .$model, .y = .$model_name,
.f = predict_values)) %>%
mutate(plot = pmap(list(df = predicted, model_name_char, add_legend, add_ylab, first),
plot_predicted))
predicted_all <- wrap_plots(models_predicted$plot) +
plot_layout(ncol = 1)
# Save predicted data to CSV
models_predicted$predicted %>%
bind_rows() %>%
write_csv(file.path(here(), "Output", "predicted_data.csv"))The figure below demonstrates the marginal effect of having negative or positive personality traits on predicted support for a given issue, conditioned on the type of frame offered to respondents. All model variables are held at their means or the following modal values:
control_modes <- data_frame("Sex" = get_mode(survey_clean$sex),
"Race" = get_mode(survey_clean$race),
"Age" = get_mode(survey_clean$age_cat),
"Democrat" = get_mode(survey_clean$democrat),
"Republican" = get_mode(survey_clean$republican)) %>%
gather(Variable, `Modal value`)
control_modes %>% pandoc.table()| Variable | Modal value |
|---|---|
| Sex | Female |
| Race | White/non-Hispanic |
| Age | 45–59 |
| Democrat | Democrat |
| Republican | Not Republican |
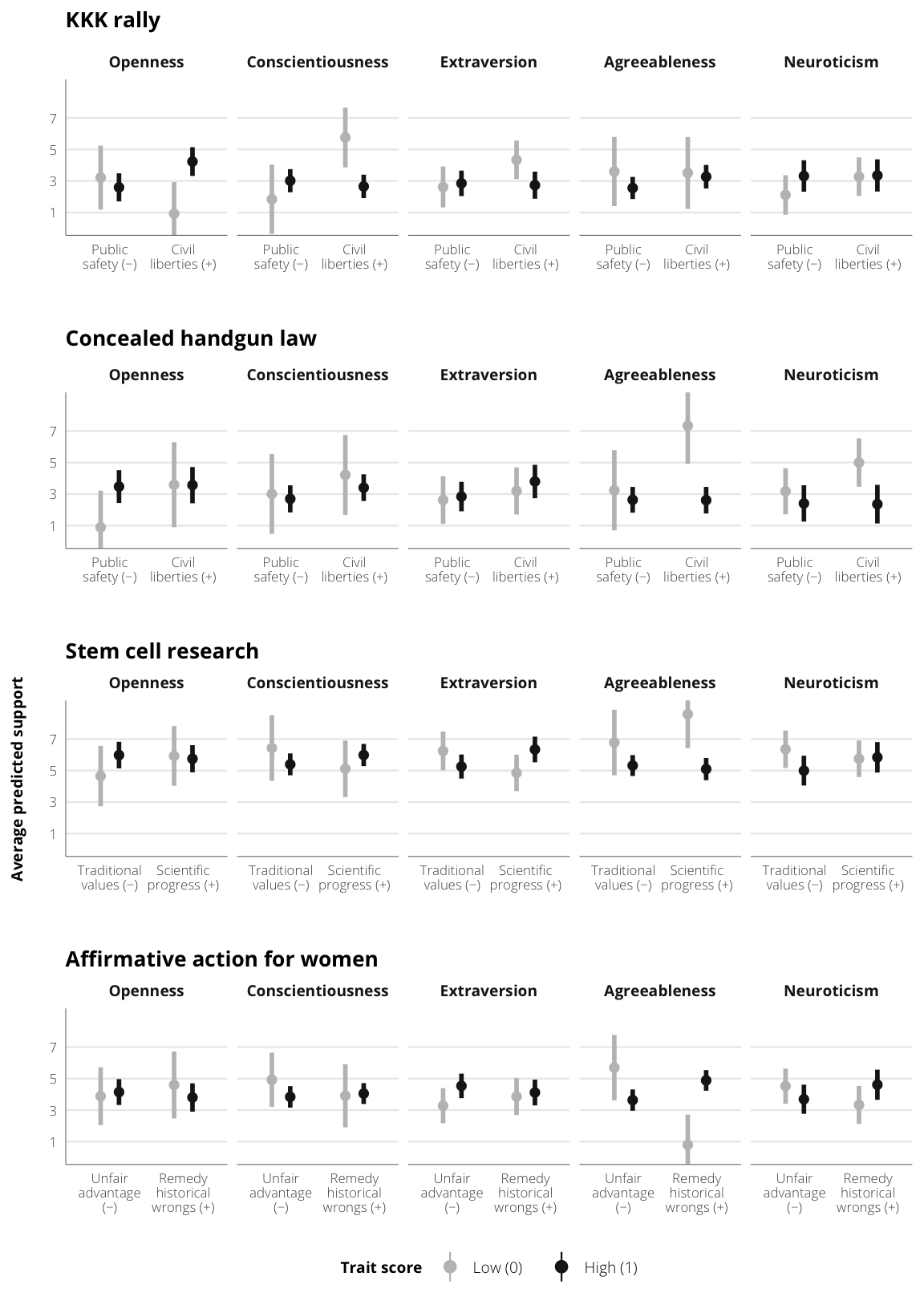
Final output
In Output/ you can find:
- Word versions of all tables (saved as
.docxfiles) - Print-ready PDF versions of all figures (saved as
.pdffiles) - High quality PNG versions of all figures (for use in Word and PowerPoint; saved as
.pngfiles) - Captions for all figures (saved as
.txtfiles)
# Convert Markdown tables to docx
capture.output({
Sys.glob(file.path(here(), "Output", "*.md")) %>%
map(~ Pandoc.convert(., format = "docx", footer = FALSE,
proc.time = FALSE, open = FALSE))
}, file = "/dev/null")
# Convert stargazer HTML tables to docx (macOS only)
if (Sys.info()['sysname'] == "Darwin" & stargazer2word) {
change.dir <- paste('cd "', file.path(here(), "bin"), '"', sep = "")
command <- paste("python3 stargazer2docx.py")
full.command <- paste(change.dir, command, sep = "; ")
system(full.command)
}LS0tCnRpdGxlOiAiTW9kZWxpbmcgc3VzY2VwdGliaWxpdHkiCmF1dGhvcjogIk1lcmVkaXRoIENvbnJveSBhbmQgQW5kcmV3IEhlaXNzIgpkYXRlOiAiYHIgZm9ybWF0KFN5cy50aW1lKCksICclQiAlZSwgJVknKWAiCmVkaXRvcl9vcHRpb25zOiAKICBjaHVua19vdXRwdXRfdHlwZTogY29uc29sZQotLS0KCmBgYHtyIHNldHVwLCBtZXNzYWdlPUZBTFNFfQprbml0cjo6b3B0c19jaHVuayRzZXQoY2FjaGUgPSBGQUxTRSwgZmlnLnJldGluYSA9IDIsCiAgICAgICAgICAgICAgICAgICAgICB0aWR5Lm9wdHMgPSBsaXN0KHdpZHRoLmN1dG9mZiA9IDEyMCksICAjIEZvciBjb2RlCiAgICAgICAgICAgICAgICAgICAgICB3aWR0aCA9IDEyMCkgICMgRm9yIG91dHB1dApgYGAKCmBgYHtyIGxvYWQtbGlicmFyaWVzLWRhdGEsIG1lc3NhZ2U9RkFMU0UsIHdhcm5pbmc9RkFMU0V9CmxpYnJhcnkodGlkeXZlcnNlKQpsaWJyYXJ5KGJyb29tKQpsaWJyYXJ5KGdnc3RhbmNlKQpsaWJyYXJ5KHBhdGNod29yaykKbGlicmFyeShwYW5kZXIpCmxpYnJhcnkoc3RhcmdhemVyKQpsaWJyYXJ5KGhlcmUpCgpzb3VyY2UoZmlsZS5wYXRoKGhlcmUoKSwgImxpYiIsICJwYW5kZXJfb3B0aW9ucy5SIikpCnNvdXJjZShmaWxlLnBhdGgoaGVyZSgpLCAibGliIiwgImdyYXBoaWNzLlIiKSkKc291cmNlKGZpbGUucGF0aChoZXJlKCksICJsaWIiLCAibGFiZWxzLlIiKSkKCnN0YXJnYXplcjJ3b3JkIDwtIEZBTFNFCgojIEJ5IGRlZmF1bHQsIFIgdXNlcyBwb2x5bm9taWFsIGNvbnRyYXN0cyBmb3Igb3JkZXJlZCBmYWN0b3JzIGluIGxpbmVhciBtb2RlbHMKIyBvcHRpb25zKCJjb250cmFzdHMiKSAKIyBTbyBtYWtlIG9yZGVyZWQgZmFjdG9ycyB1c2UgdHJlYXRtZW50IGNvbnRyYXN0cyBpbnN0ZWFkCm9wdGlvbnMoY29udHJhc3RzID0gcmVwKCJjb250ci50cmVhdG1lbnQiLCAyKSkKIyBPciBkbyBpdCBvbiBhIHNpbmdsZSB2YXJpYWJsZToKIyBjb250cmFzdHMoZGYkeCkgPC0gImNvbnRyLnRyZWF0bWVudCIKCnN1cnZleV9jbGVhbiA8LSByZWFkUkRTKGZpbGUucGF0aChoZXJlKCksICJEYXRhIiwgInN1cnZleV9jbGVhbi5yZHMiKSkKYGBgCgpgYGB7ciBoZWxwZnVsLWZ1bmN0aW9uc30KIyBDcmVhdGUgYSBuZXcgZm9ybXVsYSBiYXNlZCBvbiBhIGdpdmVuIERWIGFuZCBJVnMgKHNwZWNpZmllZCBhcyBhIGZvcm11bGFhKQpidWlsZF9mb3JtdWxhIDwtIGZ1bmN0aW9uKERWLCBJVnMpIHsKICByZWZvcm11bGF0ZShhdHRyKHRlcm1zKElWcyksICJ0ZXJtLmxhYmVscyIpLCByZXNwb25zZSA9IERWKQp9CgpnZXRfc3RhcmdhemVyX2xhYnMgPC0gZnVuY3Rpb24obW9kZWwpIHsKICBjb2VmcyA8LSB0aWR5KG1vZGVsKSAlPiUKICAgIGxlZnRfam9pbihjb2VmLm5hbWVzLCBieSA9IGMoInRlcm0iID0gImNvZWYubmFtZSIpKSAlPiUKICAgIGRpc3RpbmN0KHRlcm0sIGNvZWYuY2xlYW4pICU+JQogICAgbXV0YXRlKGNvZWYuY2xlYW4gPSBhcy5jaGFyYWN0ZXIoY29lZi5jbGVhbikpCiAgCiAgcmV0dXJuKGNvZWZzJGNvZWYuY2xlYW4pCn0KCmdldF9tb2RlIDwtIGZ1bmN0aW9uKHgpIHsKICBuYW1lcyh3aGljaC5tYXgodGFibGUoeCkpKQp9CgpwcmVkaWN0X3ZhbHVlcyA8LSBmdW5jdGlvbihtb2RlbCwgbW9kZWxfbmFtZSkgewogICMgQ2FsY3VsYXRlIHRoZSBtZWFucyBvZiBhbGwgZml2ZSBwZXJzb25hbGl0eSB0cmFpdHMgYmFzZWQgb24gdGhlIGRhdGEgdXNlZCBpbgogICMgdGhlIGdpdmVuIG1vZGVsCiAgcGVyc29uYWxpdHlfbWVhbnMgPC0gbW9kZWwkbW9kZWwgJT4lCiAgICBzdW1tYXJpc2VfYXQodmFycyhPUEVOTkVTUywgQ09OU0NJRU5USU9VU05FU1MsIEVYVFJBVkVSU0lPTiwgCiAgICAgICAgICAgICAgICAgICAgICBBR1JFRUFCTEVORVNTLCBORVVST1RJQ0lTTSksIG1lYW4pCiAgCiAgIyBSb3cgb2YgMXMKICBwZXJzb25hbGl0eV8xIDwtIGRhdGFfZnJhbWUocGVyc29uYWxpdHkgPSBjb2xuYW1lcyhwZXJzb25hbGl0eV9tZWFucyksCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIHZhbHVlID0gMSkgJT4lCiAgICBzcHJlYWQocGVyc29uYWxpdHksIHZhbHVlKQogIAogICMgUm93IG9mIDBzCiAgcGVyc29uYWxpdHlfMCA8LSBkYXRhX2ZyYW1lKHBlcnNvbmFsaXR5ID0gY29sbmFtZXMocGVyc29uYWxpdHlfbWVhbnMpLAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICB2YWx1ZSA9IDApICU+JQogICAgc3ByZWFkKHBlcnNvbmFsaXR5LCB2YWx1ZSkKICAKICAjIERhdGEgZnJhbWUgb2YgcG9zc2libGUgcGVyc29uYWxpdHkgdmFsdWVzIChtZWFuLCAwLCBhbmQgMSkKICBwZXJzb25hbGl0eV9wb3NzaWJpbGl0aWVzIDwtIGJpbmRfcm93cyhwZXJzb25hbGl0eV9tZWFucywKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICBwZXJzb25hbGl0eV8wLCBwZXJzb25hbGl0eV8xKQogIAogICMgQWxsIGNvbWJpbmF0aW9ucyBvZiBtZWFuLCAwLCBhbmQgMSBwZXJzb25hbGl0eSB2YWx1ZXMKICBuZXdfZGF0YV9wZXJzb25hbGl0aWVzIDwtIGV4cGFuZC5ncmlkKHBlcnNvbmFsaXR5X3Bvc3NpYmlsaXRpZXMpICU+JQogICAgbXV0YXRlKGlkID0gcm93X251bWJlcigpKSAlPiUKICAgIGdhdGhlcihrZXksIHZhbHVlLCAtaWQpICU+JQogICAgZ3JvdXBfYnkoaWQpICU+JQogICAgZmlsdGVyKHN1bSh2YWx1ZSA9PSAwKSA9PSAxICYgIWFueSh2YWx1ZSA9PSAxKSB8IAogICAgICAgICAgICAgc3VtKHZhbHVlID09IDEpID09IDEgJiAhYW55KHZhbHVlID09IDApKSAlPiUKICAgIHNwcmVhZChrZXksIHZhbHVlKSAlPiUKICAgIG11dGF0ZShpbmRleCA9IDEpICU+JQogICAgdW5ncm91cCgpICU+JQogICAgc2VsZWN0KC1pZCkKICAKICAjIE1lYW4gb3IgbW9kYWwgdmFsdWVzIGZvciBhbGwgb3RoZXIgbW9kZWwgSVZzCiAgY29udHJvbF9tZWFucyA8LSBkYXRhX2ZyYW1lKGluZGV4ID0gMSwgZnJhbWUgPSAwOjEsCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIHNleF9yZXYgPSBnZXRfbW9kZShzdXJ2ZXlfY2xlYW4kc2V4KSwKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgcmFjZV9yZXYgPSBnZXRfbW9kZShzdXJ2ZXlfY2xlYW4kcmFjZSksCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIGFnZV9jYXQgPSBnZXRfbW9kZShzdXJ2ZXlfY2xlYW4kYWdlX2NhdCksCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIGRlbW9jcmF0X3JldiA9IGdldF9tb2RlKHN1cnZleV9jbGVhbiRkZW1vY3JhdCksCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIHJlcHVibGljYW5fcmV2ID0gZ2V0X21vZGUoc3VydmV5X2NsZWFuJHJlcHVibGljYW4pLAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICBQT0xJVElDQUxfS05PV0xFREdFID0gbWVhbihtb2RlbCRtb2RlbCRQT0xJVElDQUxfS05PV0xFREdFKSwgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIE5DID0gbWVhbihtb2RlbCRtb2RlbCROQykpCiAgCiAgIyBBZGQgbWVhbi9tb2RhbCB2YWx1ZXMgdG8gZWFjaCBwb3NzaWJsZSBwZXJzb25hbGl0eSBjb21iaW5hdGlvbgogIG5ld19kYXRhX2Z1bGwgPC0gbmV3X2RhdGFfcGVyc29uYWxpdGllcyAlPiUKICAgIGxlZnRfam9pbihjb250cm9sX21lYW5zLCBieSA9ICJpbmRleCIpICU+JQogICAgc2VsZWN0KC1pbmRleCkKICAKICBmcmFtZV9sYWJzIDwtIGNhc2Vfd2hlbigKICAgIG1vZGVsX25hbWUgPT0gbW9kZWxfa2trX25hbWUgfiBmcmFtZV9sYWJzX2tra19ndW5zX3Bsb3QsCiAgICBtb2RlbF9uYW1lID09IG1vZGVsX2d1bnNfbmFtZSB+IGZyYW1lX2xhYnNfa2trX2d1bnNfcGxvdCwKICAgIG1vZGVsX25hbWUgPT0gbW9kZWxfc3RlbWNlbGxzX25hbWUgfiBmcmFtZV9sYWJzX3N0ZW1jZWxsc19wbG90LAogICAgbW9kZWxfbmFtZSA9PSBtb2RlbF9hZl9hY19uYW1lIH4gZnJhbWVfbGFic19hYV9wbG90CiAgKQogIAogICMgRmluYWxseSB1c2UgbmV3IGRhdGEgaW4gbW9kZWwgdG8gZ2VuZXJhdGUgcHJlZGljdGVkIHZhbHVlcwogIHBsb3RfcHJlZGljdCA8LSBhdWdtZW50KG1vZGVsLCBuZXdkYXRhID0gbmV3X2RhdGFfZnVsbCkgJT4lCiAgICBnYXRoZXIoa2V5LCB2YWx1ZSwgb25lX29mKGNvbG5hbWVzKHBlcnNvbmFsaXR5X21lYW5zKSkpICU+JQogICAgbGVmdF9qb2luKGNvZWYubmFtZXMsIGJ5ID0gYygia2V5IiA9ICJjb2VmLm5hbWUiKSkgJT4lCiAgICBmaWx0ZXIodmFsdWUgJWluJSBjKDAsIDEpKSAlPiUKICAgIG11dGF0ZSh2YWx1ZSA9IGZhY3Rvcih2YWx1ZSwgbGV2ZWxzID0gYygwLCAxKSwKICAgICAgICAgICAgICAgICAgICAgICAgICBsYWJlbHMgPSBjKCJMb3cgKDApICAgICIsICJIaWdoICgxKSIpLAogICAgICAgICAgICAgICAgICAgICAgICAgIG9yZGVyZWQgPSBUUlVFKSwKICAgICAgICAgICBmcmFtZSA9IGZhY3RvcihmcmFtZSwgbGV2ZWxzID0gYygwLCAxKSwKICAgICAgICAgICAgICAgICAgICAgICAgICBsYWJlbHMgPSBmcmFtZV9sYWJzLCBvcmRlcmVkID0gVFJVRSksCiAgICAgICAgICAgY29lZi5jbGVhbiA9IGZjdF9pbm9yZGVyKGNvZWYuY2xlYW4pLAogICAgICAgICAgIG1vZGVsX25hbWUgPSBtb2RlbF9uYW1lKQoKICByZXR1cm4ocGxvdF9wcmVkaWN0KQp9CmBgYAoKIyMgU3VzY2VwdGliaWxpdHkgdG8gaXNzdWUgZnJhbWVzCgpgYGB7ciBidWlsZC1tb2RlbHN9CiMgQmFzZSBtb2RlbCAoc2FucyBEViwgc2luY2UgdGhhdCBnZXRzIGFkZGVkIGxhdGVyKQppbmRlcF92YXJzIDwtIH4KICAjIE1haW4gY29udHJvbHMKICBzZXhfcmV2ICsgcmFjZV9yZXYgKyBhZ2VfY2F0ICsgZGVtb2NyYXRfcmV2ICsgcmVwdWJsaWNhbl9yZXYgKwogICMgRnJhbWUKICBmcmFtZSArCiAgIyBQZXJzb25hbGl0eQogIE9QRU5ORVNTICogZnJhbWUgKyAKICBDT05TQ0lFTlRJT1VTTkVTUyAqIGZyYW1lICsKICBFWFRSQVZFUlNJT04gKiBmcmFtZSArCiAgQUdSRUVBQkxFTkVTUyAqIGZyYW1lICsKICBORVVST1RJQ0lTTSAqIGZyYW1lICsKICAjIE90aGVyIHRyYWl0cwogIFBPTElUSUNBTF9LTk9XTEVER0UgKiBmcmFtZSArCiAgTkMgKiBmcmFtZQoKCiMgS0tLCmRmX2trayA8LSBzdXJ2ZXlfY2xlYW4gJT4lCiAgcmVuYW1lKGZyYW1lID0gS0tLRnJhbWVfQ2l2TGlicykKCm1vZGVsX2trayA8LSBsbShidWlsZF9mb3JtdWxhKCJLS0tfU3VwcG9ydCIsIGluZGVwX3ZhcnMpLAogICAgICAgICAgICAgICAgZGF0YSA9IGRmX2traywgd2VpZ2h0cyA9IHdlaWdodCkKCiMgR3VucwpkZl9ndW5zIDwtIHN1cnZleV9jbGVhbiAlPiUKICByZW5hbWUoZnJhbWUgPSBHdW5GcmFtZV9DaXZMaWJzKQoKbW9kZWxfZ3VucyA8LSBsbShidWlsZF9mb3JtdWxhKCJHdW5fU3VwcG9ydCIsIGluZGVwX3ZhcnMpLAogICAgICAgICAgICAgICAgIGRhdGEgPSBkZl9ndW5zLCB3ZWlnaHRzID0gd2VpZ2h0KQoKIyBTdGVtIGNlbGwgcmVzZWFyY2gKZGZfc3RlbWNlbGxzIDwtIHN1cnZleV9jbGVhbiAlPiUKICByZW5hbWUoZnJhbWUgPSBTdGVtQ2VsbHNGcmFtZV9Qb3NpdGl2ZSkKCm1vZGVsX3N0ZW1jZWxscyA8LSBsbShidWlsZF9mb3JtdWxhKCJTdGVtQ2VsbHNTdXBwb3J0IiwgaW5kZXBfdmFycyksCiAgICAgICAgICAgICAgICAgICAgICBkYXRhID0gZGZfc3RlbWNlbGxzLCB3ZWlnaHRzID0gd2VpZ2h0KQoKIyBBZmZpcm1hdGl2ZSBhY3Rpb24KZGZfYWZfYWMgPC0gc3VydmV5X2NsZWFuICU+JQogIHJlbmFtZShmcmFtZSA9IEFBRnJhbWVfcG9zaXRpdmUpCgptb2RlbF9hZl9hYyA8LSBsbShidWlsZF9mb3JtdWxhKCJBQVN1cHBvcnQiLCBpbmRlcF92YXJzKSwKICAgICAgICAgICAgICAgICAgZGF0YSA9IGRmX2FmX2FjLCB3ZWlnaHRzID0gd2VpZ2h0KQoKbW9kZWxzIDwtIHRyaWJibGUoCiAgfm1vZGVsLCB+bW9kZWxfbmFtZSwKICBtb2RlbF9ra2ssIG1vZGVsX2tra19uYW1lLAogIG1vZGVsX2d1bnMsIG1vZGVsX2d1bnNfbmFtZSwKICBtb2RlbF9zdGVtY2VsbHMsIG1vZGVsX3N0ZW1jZWxsc19uYW1lLAogIG1vZGVsX2FmX2FjLCBtb2RlbF9hZl9hY19uYW1lCikgJT4lCiAgbXV0YXRlKG1vZGVsX25hbWUgPSBmY3RfaW5vcmRlcihtb2RlbF9uYW1lLCBvcmRlcmVkID0gVFJVRSkpCmBgYAoKYGBge3IgbW9kZWxzLXBsb3QsIGZpZy53aWR0aD04LCBmaWcuaGVpZ2h0PTV9Cm1vZGVsc190aWR5IDwtIG1vZGVscyAlPiUKICBtdXRhdGUodGlkeV9tb2RlbCA9IG1vZGVsICU+JSBtYXAofiB0aWR5KC4sIGNvbmYuaW50ID0gVFJVRSkpKQoKY29lZnNfdG9fcGxvdCA8LSBjKCJPUEVOTkVTUyIsICJDT05TQ0lFTlRJT1VTTkVTUyIsICJFWFRSQVZFUlNJT04iLAogICAgICAgICAgICAgICAgICAgIkFHUkVFQUJMRU5FU1MiLCAiTkVVUk9USUNJU00iLCAiUE9MSVRJQ0FMX0tOT1dMRURHRSIsICJOQyIsCiAgICAgICAgICAgICAgICAgICAiZnJhbWU6T1BFTk5FU1MiLCAiZnJhbWU6Q09OU0NJRU5USU9VU05FU1MiLCAKICAgICAgICAgICAgICAgICAgICJmcmFtZTpFWFRSQVZFUlNJT04iLCAiZnJhbWU6QUdSRUVBQkxFTkVTUyIsIAogICAgICAgICAgICAgICAgICAgImZyYW1lOk5FVVJPVElDSVNNIiwgImZyYW1lOlBPTElUSUNBTF9LTk9XTEVER0UiLCAiZnJhbWU6TkMiKQoKZGZfY29lZl9wbG90IDwtIG1vZGVsc190aWR5ICU+JQogIHVubmVzdCh0aWR5X21vZGVsKSAlPiUKICBtdXRhdGUobG93ID0gZXN0aW1hdGUgLSBzdGQuZXJyb3IsCiAgICAgICAgIGhpZ2ggPSBlc3RpbWF0ZSArIHN0ZC5lcnJvcikgJT4lCiAgbGVmdF9qb2luKGNvZWYubmFtZXMsIGJ5ID0gYygidGVybSIgPSAiY29lZi5uYW1lIikpICU+JQogIGZpbHRlcih0ZXJtICE9ICIoSW50ZXJjZXB0KSIpICU+JQogIG11dGF0ZShjb2VmLmNsZWFuID0gZmN0X3JldihmY3RfaW5vcmRlcihjb2VmLmNsZWFuLCBvcmRlcmVkID0gVFJVRSkpLAogICAgICAgICBtb2RlbF9uYW1lID0gZmN0X3Jldihtb2RlbF9uYW1lKSkgJT4lCiAgbXV0YXRlKGZhY2V0ID0gY2FzZV93aGVuKAogICAgdGVybSAlaW4lIGNvZWZzX3RvX3Bsb3QgJiBzdHJfZGV0ZWN0KHRlcm0sICI6IikgfiAiRnJhbWUgw5dcbnBlcnNvbmFsaXR5IiwKICAgIHRlcm0gJWluJSBjb2Vmc190b19wbG90ICYgIXN0cl9kZXRlY3QodGVybSwgIjoiKSB+ICJQZXJzb25hbGl0eSIsCiAgICBUUlVFIH4gIkNvbnRyb2xzIgogICkpICU+JQogIG11dGF0ZShmYWNldCA9IGZhY3RvcihmYWNldCwgCiAgICAgICAgICAgICAgICAgICAgICAgIGxldmVscyA9IGMoIlBlcnNvbmFsaXR5IiwgIkZyYW1lIMOXXG5wZXJzb25hbGl0eSIsICJDb250cm9scyIpLAogICAgICAgICAgICAgICAgICAgICAgICBvcmRlcmVkID0gVFJVRSkpCgpjb2VmX3Bsb3QgPC0gZ2dwbG90KGRmX2NvZWZfcGxvdCwgYWVzKHggPSBlc3RpbWF0ZSwgeSA9IGNvZWYuY2xlYW4sIGNvbG91ciA9IG1vZGVsX25hbWUpKSArIAogIGdlb21fdmxpbmUoeGludGVyY2VwdCA9IDAsIGNvbG91ciA9ICJibGFjayIpICsKICBnZW9tX3BvaW50cmFuZ2VoKGFlcyh4bWluID0gbG93LCB4bWF4ID0gaGlnaCksIHNpemUgPSAwLjI1LAogICAgICAgICAgICAgICAgICAgcG9zaXRpb24gPSBwb3NpdGlvbl9kb2RnZXYoMC41KSkgKyAKICBzY2FsZV9jb2xvdXJfbWFudWFsKHZhbHVlcyA9IGZyYW1pbmcucGFsZXR0ZSgicGFsZXR0ZS5jb2xvciIpWzU6MV0pICsKICBndWlkZXMoY29sb3IgPSBndWlkZV9sZWdlbmQodGl0bGUgPSBOVUxMLCBucm93ID0gMSwgYnlyb3cgPSBUUlVFLCByZXZlcnNlID0gVFJVRSkpICsKICBsYWJzKHggPSAiQ29lZmZpY2llbnQiLCB5ID0gTlVMTCkgKwogIHRoZW1lX2ZyYW1pbmcoKSArIHRoZW1lKGxlZ2VuZC5wb3NpdGlvbiA9ICJib3R0b20iKSArCiAgZmFjZXRfd3JhcCh+IGZhY2V0LCBzY2FsZXMgPSAiZnJlZSIpCgpjb2VmX3Bsb3QKCmNhcHRpb24gPC0gYygiQ29lZmZpY2llbnRzIGZvciBhbGwgZm91ciBpc3N1ZSBtb2RlbHMiKQpzYXZlLmZpZy5jYXB0aW9uKGNvZWZfcGxvdCwgZmlsZW5hbWUgPSAiY29lZl9wbG90IiwgCiAgICAgICAgICAgICAgICAgd2lkdGggPSA4LCBoZWlnaHQgPSA1LCBjYXB0aW9uID0gY2FwdGlvbikKYGBgCgoKYGBge3IgbW9kZWxzLXNob3csIHJlc3VsdHM9ImFzaXMifQp0aXRsZSA8LSAiU3VzY2VwdGliaWxpdHkgdG8gaXNzdWUgZnJhbWVzIgpvdXQuZmlsZSA8LSBmaWxlLnBhdGgoaGVyZSgpLCAiT3V0cHV0IiwgInRhYmxlX21vZGVsX3Jlc3VsdHMuaHRtbCIpCgpzdGFyZ2F6ZXIobW9kZWxfa2trLCBtb2RlbF9ndW5zLCBtb2RlbF9zdGVtY2VsbHMsIG1vZGVsX2FmX2FjLAogICAgICAgICAgdHlwZSA9ICJodG1sIiwgZGlnaXRzID0gMiwgaW50ZXJjZXB0LmJvdHRvbSA9IEZBTFNFLAogICAgICAgICAgdGl0bGUgPSB0aXRsZSwgb3V0ID0gb3V0LmZpbGUsCiAgICAgICAgICByZXBvcnQgPSAidmMqcyIsIGRlcC52YXIuY2FwdGlvbiA9ICIiLAogICAgICAgICAgZGVwLnZhci5sYWJlbHMgPSBjKG1vZGVsX2tra19uYW1lLCBtb2RlbF9ndW5zX25hbWUsIG1vZGVsX3N0ZW1jZWxsc19uYW1lLCAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICBzdHJfcmVwbGFjZShtb2RlbF9hZl9hY19uYW1lX3Bsb3QsICJcXG4iLCAiPGJyPiIpKSwKICAgICAgICAgIGNvdmFyaWF0ZS5sYWJlbHMgPSBnZXRfc3RhcmdhemVyX2xhYnMobW9kZWxfa2trKSkKYGBgCgoKIyMgUHJlZGljdGVkIG1lYW5zCgpgYGB7ciBwbG90LXByZWRpY3RlZC1tZWFucywgd2FybmluZz1GQUxTRSwgbWVzc2FnZT1GQUxTRX0KcGxvdF9sYWJzIDwtIHRyaWJibGUoCiAgfm1vZGVsX25hbWUsIH5hZGRfbGVnZW5kLCB+YWRkX3lsYWIsIH5maXJzdCwKICBtb2RlbF9ra2tfbmFtZSwgRkFMU0UsIEZBTFNFLCBUUlVFLAogIG1vZGVsX2d1bnNfbmFtZSwgRkFMU0UsIEZBTFNFLCBGQUxTRSwKICBtb2RlbF9zdGVtY2VsbHNfbmFtZSwgRkFMU0UsIFRSVUUsIEZBTFNFLAogIG1vZGVsX2FmX2FjX25hbWUsIFRSVUUsIEZBTFNFLCBGQUxTRQopICU+JQogIG11dGF0ZShtb2RlbF9uYW1lX2NoYXIgPSBtb2RlbF9uYW1lLAogICAgICAgICBtb2RlbF9uYW1lID0gZmN0X2lub3JkZXIobW9kZWxfbmFtZSwgb3JkZXJlZCA9IFRSVUUpKQoKcGxvdF9wcmVkaWN0ZWQgPC0gZnVuY3Rpb24oZGYsIG1vZGVsX25hbWUsIGFkZF9sZWdlbmQsIGFkZF95bGFiLCBmaXJzdCkgewogIHAgPC0gZ2dwbG90KGRmLCBhZXMoeCA9IGZyYW1lLCB5ID0gLmZpdHRlZCwgY29sb3IgPSB2YWx1ZSkpICsKICAgIGdlb21fcG9pbnRyYW5nZShhZXMoeW1pbiA9IC5maXR0ZWQgKyAocW5vcm0oMC4wMjUpICogLnNlLmZpdCksCiAgICAgICAgICAgICAgICAgICAgICAgIHltYXggPSAuZml0dGVkICsgKHFub3JtKDAuOTc1KSAqIC5zZS5maXQpKSwKICAgICAgICAgICAgICAgICAgICBwb3NpdGlvbiA9IHBvc2l0aW9uX2RvZGdlKHdpZHRoID0gMC41KSwKICAgICAgICAgICAgICAgICAgICBzaXplID0gMSwgZmF0dGVuID0gMSkgKwogICAgbGFicyh4ID0gTlVMTCwgeSA9IE5VTEwsIHRpdGxlID0gbW9kZWxfbmFtZSkgKwogICAgZ3VpZGVzKGNvbG9yID0gZ3VpZGVfbGVnZW5kKHRpdGxlID0gIlRyYWl0IHNjb3JlIiwKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICBvdmVycmlkZS5hZXMgPSBsaXN0KHNpemUgPSAwLjQpKSkgKwogICAgc2NhbGVfY29sb3VyX21hbnVhbCh2YWx1ZXMgPSBmcmFtaW5nLnBhbGV0dGUoInBhbGV0dGUuYncyIiksIG5hbWUgPSBOVUxMKSArCiAgICBzY2FsZV95X2NvbnRpbnVvdXMoYnJlYWtzID0gYygxLCAzLCA1LCA3KSkgKwogICAgY29vcmRfY2FydGVzaWFuKHlsaW0gPSBjKDAsIDkpKSArCiAgICB0aGVtZV9mcmFtaW5nKCkgKyB0aGVtZShwYW5lbC5ncmlkLm1pbm9yID0gZWxlbWVudF9ibGFuaygpLAogICAgICAgICAgICAgICAgICAgICAgICAgICAgcGFuZWwuZ3JpZC5tYWpvci54ID0gZWxlbWVudF9ibGFuaygpLAogICAgICAgICAgICAgICAgICAgICAgICAgICAgc3RyaXAudGV4dCA9IGVsZW1lbnRfdGV4dChzaXplID0gcmVsKDAuOCkpLAogICAgICAgICAgICAgICAgICAgICAgICAgICAgcGxvdC50aXRsZSA9IGVsZW1lbnRfdGV4dChzaXplID0gcmVsKDEuMSkpLAogICAgICAgICAgICAgICAgICAgICAgICAgICAgYXhpcy50ZXh0ID0gZWxlbWVudF90ZXh0KHNpemUgPSByZWwoMC43KSkpICsKICAgIGZhY2V0X3dyYXAofiBjb2VmLmNsZWFuLCBucm93ID0gMSkKICAKICBpZiAoIWFkZF9sZWdlbmQpIHsKICAgIHAgPC0gcCArIGd1aWRlcyhjb2xvciA9IEZBTFNFKQogIH0gCiAgCiAgaWYgKGFkZF95bGFiKSB7CiAgICBwIDwtIHAgKyBsYWJzKHkgPSAiQXZlcmFnZSBwcmVkaWN0ZWQgc3VwcG9ydCIpCiAgfQogIAogIGlmICghZmlyc3QpIHsKICAgIHAgPC0gcCArIHRoZW1lKHBsb3QudGl0bGUgPSBlbGVtZW50X3RleHQobWFyZ2luID0gbWFyZ2luKHQgPSAyMCwgYiA9IDMpKSkKICB9CiAgCiAgcAp9Cgptb2RlbHNfcHJlZGljdGVkIDwtIG1vZGVscyAlPiUKICBsZWZ0X2pvaW4ocGxvdF9sYWJzLCBieSA9ICJtb2RlbF9uYW1lIikgJT4lCiAgbXV0YXRlKHByZWRpY3RlZCA9IG1hcDIoLnggPSAuJG1vZGVsLCAueSA9IC4kbW9kZWxfbmFtZSwgCiAgICAgICAgICAgICAgICAgICAgICAgICAgLmYgPSBwcmVkaWN0X3ZhbHVlcykpICU+JQogIG11dGF0ZShwbG90ID0gcG1hcChsaXN0KGRmID0gcHJlZGljdGVkLCBtb2RlbF9uYW1lX2NoYXIsIGFkZF9sZWdlbmQsIGFkZF95bGFiLCBmaXJzdCksCiAgICAgICAgICAgICAgICAgICAgIHBsb3RfcHJlZGljdGVkKSkKCnByZWRpY3RlZF9hbGwgPC0gd3JhcF9wbG90cyhtb2RlbHNfcHJlZGljdGVkJHBsb3QpICsgCiAgcGxvdF9sYXlvdXQobmNvbCA9IDEpCgojIFNhdmUgcHJlZGljdGVkIGRhdGEgdG8gQ1NWCm1vZGVsc19wcmVkaWN0ZWQkcHJlZGljdGVkICU+JQogIGJpbmRfcm93cygpICU+JSAKICB3cml0ZV9jc3YoZmlsZS5wYXRoKGhlcmUoKSwgIk91dHB1dCIsICJwcmVkaWN0ZWRfZGF0YS5jc3YiKSkKYGBgCgpUaGUgZmlndXJlIGJlbG93IGRlbW9uc3RyYXRlcyB0aGUgbWFyZ2luYWwgZWZmZWN0IG9mIGhhdmluZyBuZWdhdGl2ZSBvciBwb3NpdGl2ZSBwZXJzb25hbGl0eSB0cmFpdHMgb24gcHJlZGljdGVkIHN1cHBvcnQgZm9yIGEgZ2l2ZW4gaXNzdWUsIGNvbmRpdGlvbmVkIG9uIHRoZSB0eXBlIG9mIGZyYW1lIG9mZmVyZWQgdG8gcmVzcG9uZGVudHMuIEFsbCBtb2RlbCB2YXJpYWJsZXMgYXJlIGhlbGQgYXQgdGhlaXIgbWVhbnMgb3IgdGhlIGZvbGxvd2luZyBtb2RhbCB2YWx1ZXM6CgpgYGB7ciBjb250cm9sLW1vZGVzLCByZXN1bHRzPSJhc2lzIn0KY29udHJvbF9tb2RlcyA8LSBkYXRhX2ZyYW1lKCJTZXgiID0gZ2V0X21vZGUoc3VydmV5X2NsZWFuJHNleCksCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAiUmFjZSIgPSBnZXRfbW9kZShzdXJ2ZXlfY2xlYW4kcmFjZSksCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAiQWdlIiA9IGdldF9tb2RlKHN1cnZleV9jbGVhbiRhZ2VfY2F0KSwKICAgICAgICAgICAgICAgICAgICAgICAgICAgICJEZW1vY3JhdCIgPSBnZXRfbW9kZShzdXJ2ZXlfY2xlYW4kZGVtb2NyYXQpLAogICAgICAgICAgICAgICAgICAgICAgICAgICAgIlJlcHVibGljYW4iID0gZ2V0X21vZGUoc3VydmV5X2NsZWFuJHJlcHVibGljYW4pKSAlPiUKICBnYXRoZXIoVmFyaWFibGUsIGBNb2RhbCB2YWx1ZWApCgpjb250cm9sX21vZGVzICU+JSBwYW5kb2MudGFibGUoKQpgYGAKCmBgYHtyIHNob3ctcHJlZGljdGVkLCBmaWcud2lkdGg9NiwgZmlnLmhlaWdodD04LjV9CnByZWRpY3RlZF9hbGwKCmNhcHRpb24gPC0gYygiTWVhbiBwcmVkaWN0ZWQgdmFsdWVzIG9mIGlzc3VlIHN1cHBvcnQgYmFzZWQgb24gaHlwb3RoZXRpY2FsIiwgCiAgICAgICAgICAgICAicGVyc29uYWxpdHkgdHJhaXQgc2NvcmVzIGFuZCBmcmFtZSBleHBvc3VyZSIpCnNhdmUuZmlnLmNhcHRpb24ocHJlZGljdGVkX2FsbCwgZmlsZW5hbWUgPSAicHJlZGljdGVkX2FsbCIsIAogICAgICAgICAgICAgICAgIHdpZHRoID0gNiwgaGVpZ2h0ID0gOC41LCBjYXB0aW9uID0gY2FwdGlvbikKYGBgCgoKIyMgRmluYWwgb3V0cHV0CgpJbiBgT3V0cHV0L2AgeW91IGNhbiBmaW5kOgoKLSBXb3JkIHZlcnNpb25zIG9mIGFsbCB0YWJsZXMgKHNhdmVkIGFzIGAuZG9jeGAgZmlsZXMpCi0gUHJpbnQtcmVhZHkgUERGIHZlcnNpb25zIG9mIGFsbCBmaWd1cmVzIChzYXZlZCBhcyBgLnBkZmAgZmlsZXMpCi0gSGlnaCBxdWFsaXR5IFBORyB2ZXJzaW9ucyBvZiBhbGwgZmlndXJlcyAoZm9yIHVzZSBpbiBXb3JkIGFuZCBQb3dlclBvaW50OyBzYXZlZCBhcyBgLnBuZ2AgZmlsZXMpCi0gQ2FwdGlvbnMgZm9yIGFsbCBmaWd1cmVzIChzYXZlZCBhcyBgLnR4dGAgZmlsZXMpCgpgYGB7ciBjb252ZXJ0LXRhYmxlc30KIyBDb252ZXJ0IE1hcmtkb3duIHRhYmxlcyB0byBkb2N4CmNhcHR1cmUub3V0cHV0KHsKICBTeXMuZ2xvYihmaWxlLnBhdGgoaGVyZSgpLCAiT3V0cHV0IiwgIioubWQiKSkgJT4lCiAgICBtYXAofiBQYW5kb2MuY29udmVydCguLCBmb3JtYXQgPSAiZG9jeCIsIGZvb3RlciA9IEZBTFNFLAogICAgICAgICAgICAgICAgICAgICAgICAgcHJvYy50aW1lID0gRkFMU0UsIG9wZW4gPSBGQUxTRSkpCn0sIGZpbGUgPSAiL2Rldi9udWxsIikKCiMgQ29udmVydCBzdGFyZ2F6ZXIgSFRNTCB0YWJsZXMgdG8gZG9jeCAobWFjT1Mgb25seSkKaWYgKFN5cy5pbmZvKClbJ3N5c25hbWUnXSA9PSAiRGFyd2luIiAmIHN0YXJnYXplcjJ3b3JkKSB7CiAgY2hhbmdlLmRpciA8LSBwYXN0ZSgnY2QgIicsIGZpbGUucGF0aChoZXJlKCksICJiaW4iKSwgJyInLCBzZXAgPSAiIikKICBjb21tYW5kIDwtIHBhc3RlKCJweXRob24zIHN0YXJnYXplcjJkb2N4LnB5IikKICBmdWxsLmNvbW1hbmQgPC0gcGFzdGUoY2hhbmdlLmRpciwgY29tbWFuZCwgc2VwID0gIjsgIikKICBzeXN0ZW0oZnVsbC5jb21tYW5kKQp9CmBgYAo=