library(tidyverse)
library(haven)
library(stargazer)
library(broom)
library(purrr)
library(forcats)
library(viridisLite)
library(ggstance)
# By default, R uses polynomial contrasts for ordered factors in linear models
# options("contrasts")
# So make ordered factors use treatment contrasts instead
options(contrasts=rep("contr.treatment", 2))
df.crim <- readRDS("data/df_crim.rds") %>%
filter(year > 2002, year < 2016) %>%
mutate(cowcode.i = as.factor(cowcode), year.i = as.factor(year))
Our main questions: When external actors push for legal reforms, is it just a cheap response? or is there actual change? Does it matter whether domestic pressure changes domestic laws, or is it just paper compliance?
On p. 161 in Scorecard Diplomacy in “Is Criminalization Meaningful or Just Cheap Talk?”, we look just at averages. We can get better details than just averages.
TODO
Variables/data to get:
Modeling things:
- Model time since criminalization
- Can we think of another example where there has been external pressure (perhaps from a treaty) to implement reforms, and where we can consider implementing legislation.
- Is there a way to do mediation analysis? Is criminalization mediating the effects of the palermo protocol or of tier pressure — or a combination?
Other issues
- Partial vs. full criminalization
- Figure 6.8 from the book - look at two of the three Ps (not prosecution) as DVs in Cho’s models
- Also code if countries have an action plan or not - that might matter too - control for US effort (not the TIP score, but other measures of aid, like Wikileaks, USAID, number of trafficking NGOs in the country, etc.)
Run models
For now, we just add the degree of criminalization as a continuous variable (0–2) to the original Cho OLS models.
model1 <- lm(prot_prev ~ prot_prev_lag + crim.level_lag +
corruption + polity + female.leg.prop + wecon +
palermo.ratified + gdp.capita_log + us.aid.pct.gdp +
year.i + cowcode.i,
data = df.crim)
model2 <- lm(prevention ~ prevention_lag + crim.level_lag +
corruption + polity + female.leg.prop + wecon +
palermo.ratified + gdp.capita_log + us.aid.pct.gdp +
year.i + cowcode.i,
data = df.crim)
model3 <- lm(protection ~ protection_lag + crim.level_lag +
corruption + polity + female.leg.prop + wecon +
palermo.ratified + gdp.capita_log + us.aid.pct.gdp +
year.i + cowcode.i,
data = df.crim)
model4 <- lm(prot_prev ~ prot_prev_lag2 + crim.level_lag2 +
corruption + polity + female.leg.prop + wecon +
palermo.ratified + gdp.capita_log + us.aid.pct.gdp +
year.i + cowcode.i,
data = df.crim)
model5 <- lm(prevention ~ prevention_lag2 + crim.level_lag2 +
corruption + polity + female.leg.prop + wecon +
palermo.ratified + gdp.capita_log + us.aid.pct.gdp +
year.i + cowcode.i,
data = df.crim)
model6 <- lm(protection ~ protection_lag2 + crim.level_lag2 +
corruption + polity + female.leg.prop + wecon +
palermo.ratified + gdp.capita_log + us.aid.pct.gdp +
year.i + cowcode.i,
data = df.crim)
Preliminarily it looks like criminalization matters substantially. Moving from 0 to 1 (or 1 to 2) in the preceding year is associated with a 0.14 point increase in the protection + prevention indexes and a 0.1 point increase in the protection index. The effect is positive for prevention, but not significant.
models <- list(model1, model2, model3, model4, model5, model6)
num.models <- length(models)
var.labs <- c("Protection + prevention (t − 1)", "Prevention (t − 1)",
"Protection (t − 1)", "**Criminalization (t - 1)**",
"Protection + prevention (t − 2)", "Prevention (t − 2)",
"Protection (t − 2)", "**Criminalization (t - 2)**",
"Control of corruption", "Democracy",
"Women legislators (%)", "Women economic rights",
"Palermo Protocol ratified", "GDP per capita (log)",
"US aid (% of GDP)")
dep.var.labels <- c("Protection + Prevention", "Prevention", "Protection",
"Protection + Prevention", "Prevention", "Protection")
col.labs <- sprintf("(%s)", 1:num.models)
extra.lines <- list(c("Model type",
rep("OLS", num.models)),
c("Country fixed effects",
rep("Yes", num.models)),
c("Year fixed effects",
rep("Yes", num.models)))
title <- "Checking for the effect of criminalization"
stargazer(models,
type = "html", omit = c("cow", "Constant", "year"),
add.lines = extra.lines, title = title, covariate.labels = var.labs,
dep.var.labels = dep.var.labels, dep.var.caption = "",
keep.stat = c("n", "adj.rsq"),
model.numbers = FALSE, column.labels = col.labs,
model.names = FALSE, dep.var.labels.include = TRUE)
Checking for the effect of criminalization
|
|
|
|
Protection + Prevention
|
Prevention
|
Protection
|
Protection + Prevention
|
Prevention
|
Protection
|
|
|
(1)
|
(2)
|
(3)
|
(4)
|
(5)
|
(6)
|
|
|
|
Protection + prevention (t − 1)
|
0.330***
|
|
|
|
|
|
|
|
(0.029)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Prevention (t − 1)
|
|
0.255***
|
|
|
|
|
|
|
|
(0.030)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Protection (t − 1)
|
|
|
0.283***
|
|
|
|
|
|
|
|
(0.029)
|
|
|
|
|
|
|
|
|
|
|
|
|
Criminalization (t - 1)
|
0.138**
|
0.053
|
0.106***
|
|
|
|
|
|
(0.059)
|
(0.038)
|
(0.040)
|
|
|
|
|
|
|
|
|
|
|
|
|
Protection + prevention (t − 2)
|
|
|
|
0.040
|
|
|
|
|
|
|
|
(0.031)
|
|
|
|
|
|
|
|
|
|
|
|
Prevention (t − 2)
|
|
|
|
|
-0.058*
|
|
|
|
|
|
|
|
(0.032)
|
|
|
|
|
|
|
|
|
|
|
Protection (t − 2)
|
|
|
|
|
|
0.073**
|
|
|
|
|
|
|
|
(0.031)
|
|
|
|
|
|
|
|
|
|
Criminalization (t - 2)
|
|
|
|
0.145**
|
0.020
|
0.127***
|
|
|
|
|
|
(0.063)
|
(0.039)
|
(0.042)
|
|
|
|
|
|
|
|
|
|
Control of corruption
|
0.355*
|
0.261**
|
0.111
|
0.472**
|
0.408***
|
0.102
|
|
|
(0.202)
|
(0.130)
|
(0.137)
|
(0.220)
|
(0.138)
|
(0.146)
|
|
|
|
|
|
|
|
|
|
Democracy
|
-0.004
|
0.018
|
-0.024
|
-0.005
|
0.020
|
-0.026*
|
|
|
(0.021)
|
(0.014)
|
(0.014)
|
(0.023)
|
(0.014)
|
(0.015)
|
|
|
|
|
|
|
|
|
|
Women legislators (%)
|
-0.001
|
-0.001
|
0.0003
|
-0.002
|
-0.002
|
0.001
|
|
|
(0.003)
|
(0.002)
|
(0.002)
|
(0.004)
|
(0.002)
|
(0.002)
|
|
|
|
|
|
|
|
|
|
Women economic rights
|
0.006
|
0.073*
|
-0.072*
|
-0.002
|
0.081*
|
-0.087*
|
|
|
(0.063)
|
(0.040)
|
(0.043)
|
(0.067)
|
(0.042)
|
(0.045)
|
|
|
|
|
|
|
|
|
|
Palermo Protocol ratified
|
0.144
|
0.102
|
0.051
|
0.315***
|
0.167**
|
0.149*
|
|
|
(0.108)
|
(0.069)
|
(0.073)
|
(0.119)
|
(0.074)
|
(0.079)
|
|
|
|
|
|
|
|
|
|
GDP per capita (log)
|
0.663*
|
0.671***
|
0.025
|
0.720*
|
0.759***
|
0.022
|
|
|
(0.340)
|
(0.219)
|
(0.229)
|
(0.376)
|
(0.235)
|
(0.247)
|
|
|
|
|
|
|
|
|
|
US aid (% of GDP)
|
2.939
|
2.869
|
-0.359
|
-1.070
|
-0.894
|
-0.566
|
|
|
(3.930)
|
(2.527)
|
(2.262)
|
(3.553)
|
(2.221)
|
(2.365)
|
|
|
|
|
|
|
|
|
|
|
|
Model type
|
OLS
|
OLS
|
OLS
|
OLS
|
OLS
|
OLS
|
|
Country fixed effects
|
Yes
|
Yes
|
Yes
|
Yes
|
Yes
|
Yes
|
|
Year fixed effects
|
Yes
|
Yes
|
Yes
|
Yes
|
Yes
|
Yes
|
|
Observations
|
1,234
|
1,235
|
1,239
|
1,166
|
1,168
|
1,173
|
|
Adjusted R2
|
0.756
|
0.646
|
0.665
|
0.730
|
0.630
|
0.644
|
|
|
|
Note:
|
p<0.1; p<0.05; p<0.01
|
Estimating direct effects
Example using Fearon and Laitin 2003
# Panel-based lags (but tidyverse is way easier than this...)
pan.lag <- function(x, ind, lag = 1) {
unlist(tapply(x,ind, function(x) c(rep(NA, times = lag),x[-((length(x) - lag +1):length(x))])))
}
# Load and clean data
fearon <- read_dta("data/repdata.dta")
fearon_subset <- filter(fearon, onset < 4) %>%
mutate(instab2 = 1 * (abs(polity2l - pan.lag(polity2, ccode, 2)) > 3))
# Baseline model
baseline <- lm(onset ~ lmtnest + ncontig + Oil + ethfrac + relfrac,
data = fearon_subset)
# summary(baseline)
# Baseline model +
ptbias <- lm(onset ~ lmtnest + ncontig + Oil +
ethfrac + relfrac + instab2,
data = fearon_subset)
# summary(ptbias)
# First stage (to get effect of instability)
first <- lm(onset ~ warl + gdpenl + lpop + lmtnest +
ncontig + Oil + nwstate + instab + polity2l + ethfrac + relfrac,
data = fearon_subset)
# summary(first)
# Second stage (CDE of ethfrac without instability)
direct <- lm(I(onset - coef(first)["instab"] * instab) ~ lmtnest + ncontig +
Oil + ethfrac + relfrac,
data = fearon_subset)
# summary(direct)
coefs <- tribble(
~model_name, ~model,
"Baseline", baseline,
"With instability", ptbias,
"Fearon and Laitin", first,
"ACDE", direct) %>%
mutate(tidified = model %>% map(~ tidy(., conf.int = TRUE))) %>%
unnest(tidified)
to_plot <- coefs %>%
filter(term == "ethfrac") %>%
mutate(model_name = fct_rev(fct_inorder(model_name)))
ggplot(to_plot, aes(x = estimate, y = model_name, color = model_name)) +
geom_pointrangeh(aes(xmin = conf.low, xmax = conf.high)) +
geom_vline(xintercept = 0) +
scale_color_viridis_d(option = "magma", end = 0.9, guide = FALSE) +
labs(x = "Estimate", y = NULL) +
theme_light()
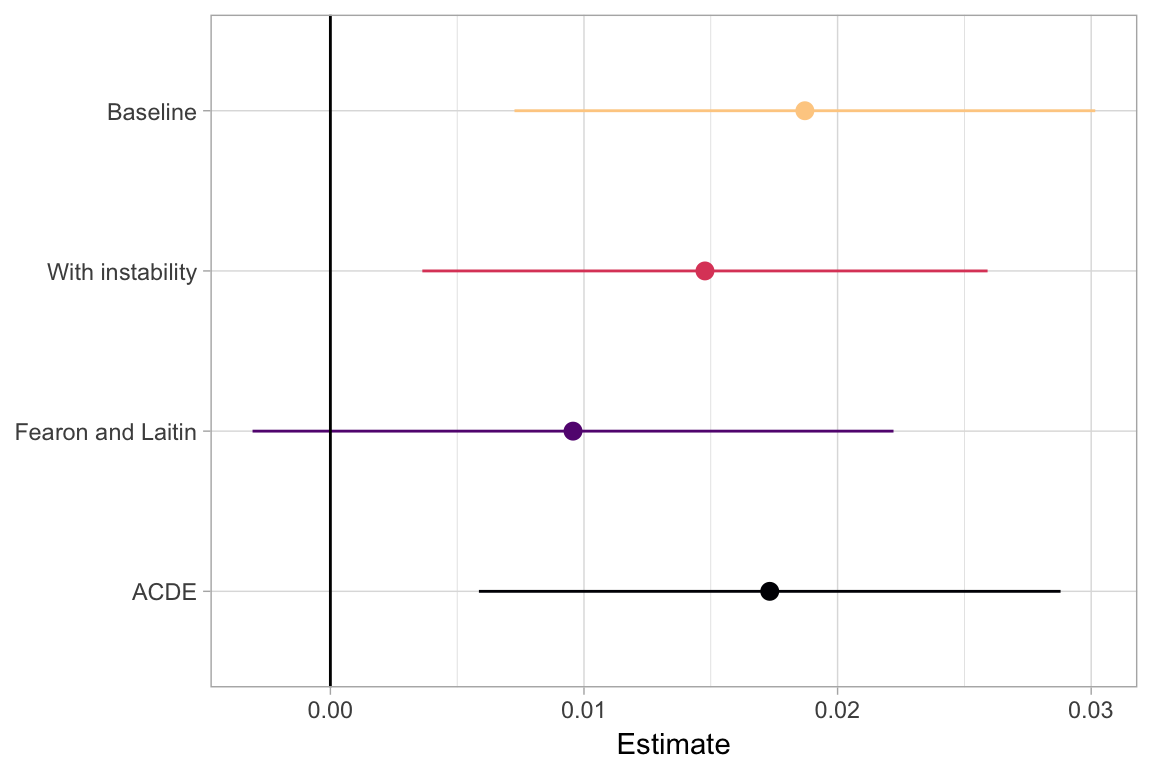
Our own average controlled direct effect estimation
If we want to do the same ACDE estimation, we have to distinguish between these types of variables:
- Pretreatment confounders
- Intermediate confounders
- Posttreatment variables
LS0tCnRpdGxlOiAiRWZmZWN0IG9mIGNyaW1pbmFsaXphdGlvbiIKZGF0ZTogImByIGZvcm1hdChTeXMudGltZSgpLCAnJUYnKWAiCmVkaXRvcl9vcHRpb25zOiAKICBjaHVua19vdXRwdXRfdHlwZTogY29uc29sZQotLS0KCmBgYHtyIHNldHVwLCBpbmNsdWRlPUZBTFNFfQprbml0cjo6b3B0c19jaHVuayRzZXQoZmlnLnJldGluYSA9IDIsCiAgICAgICAgICAgICAgICAgICAgICB0aWR5Lm9wdHM9bGlzdCh3aWR0aC5jdXRvZmYgPSAxMDApLCAgIyBGb3IgY29kZQogICAgICAgICAgICAgICAgICAgICAgb3B0aW9ucyh3aWR0aCA9IDEwMCkpICAjIEZvciBvdXRwdXQKYGBgCgpgYGB7ciBsb2FkLWxpYnJhcmllcywgbWVzc2FnZT1GQUxTRX0KbGlicmFyeSh0aWR5dmVyc2UpCmxpYnJhcnkoaGF2ZW4pCmxpYnJhcnkoc3RhcmdhemVyKQpsaWJyYXJ5KGJyb29tKQpsaWJyYXJ5KHB1cnJyKQpsaWJyYXJ5KGZvcmNhdHMpCmxpYnJhcnkodmlyaWRpc0xpdGUpCmxpYnJhcnkoZ2dzdGFuY2UpCgojIEJ5IGRlZmF1bHQsIFIgdXNlcyBwb2x5bm9taWFsIGNvbnRyYXN0cyBmb3Igb3JkZXJlZCBmYWN0b3JzIGluIGxpbmVhciBtb2RlbHMKIyBvcHRpb25zKCJjb250cmFzdHMiKSAKIyBTbyBtYWtlIG9yZGVyZWQgZmFjdG9ycyB1c2UgdHJlYXRtZW50IGNvbnRyYXN0cyBpbnN0ZWFkCm9wdGlvbnMoY29udHJhc3RzPXJlcCgiY29udHIudHJlYXRtZW50IiwgMikpCmBgYAoKYGBge3IgbG9hZC1kYXRhfQpkZi5jcmltIDwtIHJlYWRSRFMoImRhdGEvZGZfY3JpbS5yZHMiKSAlPiUKICBmaWx0ZXIoeWVhciA+IDIwMDIsIHllYXIgPCAyMDE2KSAlPiUKICBtdXRhdGUoY293Y29kZS5pID0gYXMuZmFjdG9yKGNvd2NvZGUpLCB5ZWFyLmkgPSBhcy5mYWN0b3IoeWVhcikpCmBgYAoKKipPdXIgbWFpbiBxdWVzdGlvbnMqKjogV2hlbiBleHRlcm5hbCBhY3RvcnMgcHVzaCBmb3IgbGVnYWwgcmVmb3JtcywgaXMgaXQganVzdCBhIGNoZWFwIHJlc3BvbnNlPyBvciBpcyB0aGVyZSBhY3R1YWwgY2hhbmdlPyBEb2VzIGl0IG1hdHRlciB3aGV0aGVyIGRvbWVzdGljIHByZXNzdXJlIGNoYW5nZXMgZG9tZXN0aWMgbGF3cywgb3IgaXMgaXQganVzdCBwYXBlciBjb21wbGlhbmNlPwoKT24gcC4gMTYxIGluICpTY29yZWNhcmQgRGlwbG9tYWN5KiBpbiAiSXMgQ3JpbWluYWxpemF0aW9uIE1lYW5pbmdmdWwgb3IgSnVzdCBDaGVhcCBUYWxrPyIsIHdlIGxvb2sganVzdCBhdCBhdmVyYWdlcy4gV2UgY2FuIGdldCBiZXR0ZXIgZGV0YWlscyB0aGFuIGp1c3QgYXZlcmFnZXMuCgoKIyMgVE9ETwoKVmFyaWFibGVzL2RhdGEgdG8gZ2V0OgoKLSBQcmVzZW5jZS9hYnNlbmNlIG9mIGFjdGlvbiBwbGFuCi0gUmljaGFyZCBGcmFuaydzIGRhdGEgKDxodHRwczovL2h1bWFudHJhZmZpY2tpbmdpbmRpY2F0b3JzLm9yZy8+KQotIE5HTyBkZW5zaXR5Ci0gWWVhcnMgc2luY2UgY3JpbWluYWxpemF0aW9uCgpNb2RlbGluZyB0aGluZ3M6CgotIE1vZGVsIHRpbWUgc2luY2UgY3JpbWluYWxpemF0aW9uCi0gQ2FuIHdlIHRoaW5rIG9mIGFub3RoZXIgZXhhbXBsZSB3aGVyZSB0aGVyZSBoYXMgYmVlbiBleHRlcm5hbCBwcmVzc3VyZSAocGVyaGFwcyBmcm9tIGEgdHJlYXR5KSB0byBpbXBsZW1lbnQgcmVmb3JtcywgYW5kIHdoZXJlIHdlIGNhbiBjb25zaWRlciBpbXBsZW1lbnRpbmcgbGVnaXNsYXRpb24uCi0gSXMgdGhlcmUgYSB3YXkgdG8gZG8gbWVkaWF0aW9uIGFuYWx5c2lzPyBJcyBjcmltaW5hbGl6YXRpb24gbWVkaWF0aW5nIHRoZSBlZmZlY3RzIG9mIHRoZSBwYWxlcm1vIHByb3RvY29sIG9yIG9mIHRpZXIgcHJlc3N1cmUg4oCUIG9yIGEgY29tYmluYXRpb24/CgpPdGhlciBpc3N1ZXMKCi0gUGFydGlhbCB2cy4gZnVsbCBjcmltaW5hbGl6YXRpb24KLSBGaWd1cmUgNi44IGZyb20gdGhlIGJvb2sgLSBsb29rIGF0IHR3byBvZiB0aGUgdGhyZWUgUHMgKG5vdCBwcm9zZWN1dGlvbikgYXMgRFZzIGluIENob+KAmXMgbW9kZWxzCi0gQWxzbyBjb2RlIGlmIGNvdW50cmllcyBoYXZlIGFuIGFjdGlvbiBwbGFuIG9yIG5vdCAtIHRoYXQgbWlnaHQgbWF0dGVyIHRvbyAtIGNvbnRyb2wgZm9yIFVTIGVmZm9ydCAobm90IHRoZSBUSVAgc2NvcmUsIGJ1dCBvdGhlciBtZWFzdXJlcyBvZiBhaWQsIGxpa2UgV2lraWxlYWtzLCBVU0FJRCwgbnVtYmVyIG9mIHRyYWZmaWNraW5nIE5HT3MgaW4gdGhlIGNvdW50cnksIGV0Yy4pCgoKIyMgUnVuIG1vZGVscwoKRm9yIG5vdywgd2UganVzdCBhZGQgdGhlIGRlZ3JlZSBvZiBjcmltaW5hbGl6YXRpb24gYXMgYSBjb250aW51b3VzIHZhcmlhYmxlICgw4oCTMikgdG8gdGhlIG9yaWdpbmFsIENobyBPTFMgbW9kZWxzLgoKYGBge3IgY3JpbS1lZmZlY3R9Cm1vZGVsMSA8LSBsbShwcm90X3ByZXYgfiBwcm90X3ByZXZfbGFnICsgY3JpbS5sZXZlbF9sYWcgKyAKICAgICAgICAgICAgICAgY29ycnVwdGlvbiArIHBvbGl0eSArIGZlbWFsZS5sZWcucHJvcCArIHdlY29uICsgCiAgICAgICAgICAgICAgIHBhbGVybW8ucmF0aWZpZWQgKyBnZHAuY2FwaXRhX2xvZyArIHVzLmFpZC5wY3QuZ2RwICsgCiAgICAgICAgICAgICAgIHllYXIuaSArIGNvd2NvZGUuaSwgCiAgICAgICAgICAgICBkYXRhID0gZGYuY3JpbSkKCm1vZGVsMiA8LSBsbShwcmV2ZW50aW9uIH4gcHJldmVudGlvbl9sYWcgKyBjcmltLmxldmVsX2xhZyArIAogICAgICAgICAgICAgICBjb3JydXB0aW9uICsgcG9saXR5ICsgZmVtYWxlLmxlZy5wcm9wICsgd2Vjb24gKyAKICAgICAgICAgICAgICAgcGFsZXJtby5yYXRpZmllZCArIGdkcC5jYXBpdGFfbG9nICsgdXMuYWlkLnBjdC5nZHAgKyAKICAgICAgICAgICAgICAgeWVhci5pICsgY293Y29kZS5pLCAKICAgICAgICAgICAgIGRhdGEgPSBkZi5jcmltKQoKbW9kZWwzIDwtIGxtKHByb3RlY3Rpb24gfiBwcm90ZWN0aW9uX2xhZyArIGNyaW0ubGV2ZWxfbGFnICsgCiAgICAgICAgICAgICAgIGNvcnJ1cHRpb24gKyBwb2xpdHkgKyBmZW1hbGUubGVnLnByb3AgKyB3ZWNvbiArIAogICAgICAgICAgICAgICBwYWxlcm1vLnJhdGlmaWVkICsgZ2RwLmNhcGl0YV9sb2cgKyB1cy5haWQucGN0LmdkcCArIAogICAgICAgICAgICAgICB5ZWFyLmkgKyBjb3djb2RlLmksIAogICAgICAgICAgICAgZGF0YSA9IGRmLmNyaW0pCgptb2RlbDQgPC0gbG0ocHJvdF9wcmV2IH4gcHJvdF9wcmV2X2xhZzIgKyBjcmltLmxldmVsX2xhZzIgKyAKICAgICAgICAgICAgICAgY29ycnVwdGlvbiArIHBvbGl0eSArIGZlbWFsZS5sZWcucHJvcCArIHdlY29uICsgCiAgICAgICAgICAgICAgIHBhbGVybW8ucmF0aWZpZWQgKyBnZHAuY2FwaXRhX2xvZyArIHVzLmFpZC5wY3QuZ2RwICsgCiAgICAgICAgICAgICAgIHllYXIuaSArIGNvd2NvZGUuaSwgCiAgICAgICAgICAgICBkYXRhID0gZGYuY3JpbSkKCm1vZGVsNSA8LSBsbShwcmV2ZW50aW9uIH4gcHJldmVudGlvbl9sYWcyICsgY3JpbS5sZXZlbF9sYWcyICsgCiAgICAgICAgICAgICAgIGNvcnJ1cHRpb24gKyBwb2xpdHkgKyBmZW1hbGUubGVnLnByb3AgKyB3ZWNvbiArIAogICAgICAgICAgICAgICBwYWxlcm1vLnJhdGlmaWVkICsgZ2RwLmNhcGl0YV9sb2cgKyB1cy5haWQucGN0LmdkcCArIAogICAgICAgICAgICAgICB5ZWFyLmkgKyBjb3djb2RlLmksIAogICAgICAgICAgICAgZGF0YSA9IGRmLmNyaW0pCgptb2RlbDYgPC0gbG0ocHJvdGVjdGlvbiB+IHByb3RlY3Rpb25fbGFnMiArIGNyaW0ubGV2ZWxfbGFnMiArIAogICAgICAgICAgICAgICBjb3JydXB0aW9uICsgcG9saXR5ICsgZmVtYWxlLmxlZy5wcm9wICsgd2Vjb24gKyAKICAgICAgICAgICAgICAgcGFsZXJtby5yYXRpZmllZCArIGdkcC5jYXBpdGFfbG9nICsgdXMuYWlkLnBjdC5nZHAgKyAKICAgICAgICAgICAgICAgeWVhci5pICsgY293Y29kZS5pLCAKICAgICAgICAgICAgIGRhdGEgPSBkZi5jcmltKQpgYGAKClByZWxpbWluYXJpbHkgaXQgbG9va3MgbGlrZSBjcmltaW5hbGl6YXRpb24gbWF0dGVycyBzdWJzdGFudGlhbGx5LiBNb3ZpbmcgZnJvbSAwIHRvIDEgKG9yIDEgdG8gMikgaW4gdGhlIHByZWNlZGluZyB5ZWFyIGlzIGFzc29jaWF0ZWQgd2l0aCBhIDAuMTQgcG9pbnQgaW5jcmVhc2UgaW4gdGhlIHByb3RlY3Rpb24gKyBwcmV2ZW50aW9uIGluZGV4ZXMgYW5kIGEgMC4xIHBvaW50IGluY3JlYXNlIGluIHRoZSBwcm90ZWN0aW9uIGluZGV4LiBUaGUgZWZmZWN0IGlzIHBvc2l0aXZlIGZvciBwcmV2ZW50aW9uLCBidXQgbm90IHNpZ25pZmljYW50LgoKYGBge3IgZGlzcGxheS1jcmltLWVmZmVjdCwgcmVzdWx0cz0iYXNpcyJ9Cm1vZGVscyA8LSBsaXN0KG1vZGVsMSwgbW9kZWwyLCBtb2RlbDMsIG1vZGVsNCwgbW9kZWw1LCBtb2RlbDYpCgpudW0ubW9kZWxzIDwtIGxlbmd0aChtb2RlbHMpCgp2YXIubGFicyA8LSBjKCJQcm90ZWN0aW9uICsgcHJldmVudGlvbiAodCDiiJIgMSkiLCAiUHJldmVudGlvbiAodCDiiJIgMSkiLCAKICAgICAgICAgICAgICAiUHJvdGVjdGlvbiAodCDiiJIgMSkiLCAiKipDcmltaW5hbGl6YXRpb24gKHQgLSAxKSoqIiwKICAgICAgICAgICAgICAiUHJvdGVjdGlvbiArIHByZXZlbnRpb24gKHQg4oiSIDIpIiwgIlByZXZlbnRpb24gKHQg4oiSIDIpIiwgCiAgICAgICAgICAgICAgIlByb3RlY3Rpb24gKHQg4oiSIDIpIiwgIioqQ3JpbWluYWxpemF0aW9uICh0IC0gMikqKiIsCiAgICAgICAgICAgICAgIkNvbnRyb2wgb2YgY29ycnVwdGlvbiIsICJEZW1vY3JhY3kiLCAKICAgICAgICAgICAgICAiV29tZW4gbGVnaXNsYXRvcnMgKCUpIiwgIldvbWVuIGVjb25vbWljIHJpZ2h0cyIsCiAgICAgICAgICAgICAgIlBhbGVybW8gUHJvdG9jb2wgcmF0aWZpZWQiLCAiR0RQIHBlciBjYXBpdGEgKGxvZykiLCAKICAgICAgICAgICAgICAiVVMgYWlkICglIG9mIEdEUCkiKQoKZGVwLnZhci5sYWJlbHMgPC0gYygiUHJvdGVjdGlvbiArIFByZXZlbnRpb24iLCAiUHJldmVudGlvbiIsICJQcm90ZWN0aW9uIiwKICAgICAgICAgICAgICAgICAgICAiUHJvdGVjdGlvbiArIFByZXZlbnRpb24iLCAiUHJldmVudGlvbiIsICJQcm90ZWN0aW9uIikKCmNvbC5sYWJzIDwtIHNwcmludGYoIiglcykiLCAxOm51bS5tb2RlbHMpCgpleHRyYS5saW5lcyA8LSBsaXN0KGMoIk1vZGVsIHR5cGUiLAogICAgICAgICAgICAgICAgICAgICAgcmVwKCJPTFMiLCBudW0ubW9kZWxzKSksCiAgICAgICAgICAgICAgICAgICAgYygiQ291bnRyeSBmaXhlZCBlZmZlY3RzIiwKICAgICAgICAgICAgICAgICAgICAgIHJlcCgiWWVzIiwgbnVtLm1vZGVscykpLAogICAgICAgICAgICAgICAgICAgIGMoIlllYXIgZml4ZWQgZWZmZWN0cyIsCiAgICAgICAgICAgICAgICAgICAgICByZXAoIlllcyIsIG51bS5tb2RlbHMpKSkKCnRpdGxlIDwtICJDaGVja2luZyBmb3IgdGhlIGVmZmVjdCBvZiBjcmltaW5hbGl6YXRpb24iCgpzdGFyZ2F6ZXIobW9kZWxzLCAKICAgICAgICAgIHR5cGUgPSAiaHRtbCIsIG9taXQgPSBjKCJjb3ciLCAiQ29uc3RhbnQiLCAieWVhciIpLCAKICAgICAgICAgIGFkZC5saW5lcyA9IGV4dHJhLmxpbmVzLCB0aXRsZSA9IHRpdGxlLCBjb3ZhcmlhdGUubGFiZWxzID0gdmFyLmxhYnMsCiAgICAgICAgICBkZXAudmFyLmxhYmVscyA9IGRlcC52YXIubGFiZWxzLCBkZXAudmFyLmNhcHRpb24gPSAiIiwKICAgICAgICAgIGtlZXAuc3RhdCA9IGMoIm4iLCAiYWRqLnJzcSIpLAogICAgICAgICAgbW9kZWwubnVtYmVycyA9IEZBTFNFLCBjb2x1bW4ubGFiZWxzID0gY29sLmxhYnMsIAogICAgICAgICAgbW9kZWwubmFtZXMgPSBGQUxTRSwgZGVwLnZhci5sYWJlbHMuaW5jbHVkZSA9IFRSVUUpCmBgYAoKCiMjIEVzdGltYXRpbmcgZGlyZWN0IGVmZmVjdHMKCiMjIyBFeGFtcGxlIHVzaW5nIEZlYXJvbiBhbmQgTGFpdGluIDIwMDMKCmBgYHtyfQojIFBhbmVsLWJhc2VkIGxhZ3MgKGJ1dCB0aWR5dmVyc2UgaXMgd2F5IGVhc2llciB0aGFuIHRoaXMuLi4pCnBhbi5sYWcgPC0gZnVuY3Rpb24oeCwgaW5kLCBsYWcgPSAxKSB7CiAgdW5saXN0KHRhcHBseSh4LGluZCwgZnVuY3Rpb24oeCkgYyhyZXAoTkEsIHRpbWVzID0gbGFnKSx4Wy0oKGxlbmd0aCh4KSAtIGxhZyArMSk6bGVuZ3RoKHgpKV0pKSkKfQoKIyBMb2FkIGFuZCBjbGVhbiBkYXRhCmZlYXJvbiA8LSByZWFkX2R0YSgiZGF0YS9yZXBkYXRhLmR0YSIpCmZlYXJvbl9zdWJzZXQgPC0gZmlsdGVyKGZlYXJvbiwgb25zZXQgPCA0KSAlPiUKICBtdXRhdGUoaW5zdGFiMiA9IDEgKiAoYWJzKHBvbGl0eTJsIC0gcGFuLmxhZyhwb2xpdHkyLCBjY29kZSwgMikpID4gMykpCgojIEJhc2VsaW5lIG1vZGVsCmJhc2VsaW5lIDwtIGxtKG9uc2V0IH4gIGxtdG5lc3QgKyBuY29udGlnICsgT2lsICsgZXRoZnJhYyArIHJlbGZyYWMsCiAgICAgICAgICAgICAgIGRhdGEgPSBmZWFyb25fc3Vic2V0KQojIHN1bW1hcnkoYmFzZWxpbmUpCgojIEJhc2VsaW5lIG1vZGVsICsgCnB0YmlhcyA8LSBsbShvbnNldCB+ICBsbXRuZXN0ICsgbmNvbnRpZyAgKyBPaWwgKyAKICAgICAgICAgICAgICAgZXRoZnJhYyArIHJlbGZyYWMgKyBpbnN0YWIyLCAKICAgICAgICAgICAgIGRhdGEgPSBmZWFyb25fc3Vic2V0KQojIHN1bW1hcnkocHRiaWFzKQoKIyBGaXJzdCBzdGFnZSAodG8gZ2V0IGVmZmVjdCBvZiBpbnN0YWJpbGl0eSkKZmlyc3QgPC0gbG0ob25zZXQgfiB3YXJsICsgZ2RwZW5sICsgbHBvcCArIGxtdG5lc3QgKwogICAgICAgICAgICAgIG5jb250aWcgKyBPaWwgKyBud3N0YXRlICsgaW5zdGFiICsgcG9saXR5MmwgKyBldGhmcmFjICsgcmVsZnJhYywKICAgICAgICAgICAgZGF0YSA9IGZlYXJvbl9zdWJzZXQpCiMgc3VtbWFyeShmaXJzdCkKCiMgU2Vjb25kIHN0YWdlIChDREUgb2YgZXRoZnJhYyB3aXRob3V0IGluc3RhYmlsaXR5KQpkaXJlY3QgPC0gbG0oSShvbnNldCAtIGNvZWYoZmlyc3QpWyJpbnN0YWIiXSAqIGluc3RhYikgfiBsbXRuZXN0ICsgbmNvbnRpZyArIAogICAgICAgICAgICAgICBPaWwgKyBldGhmcmFjICsgcmVsZnJhYywKICAgICAgICAgICAgIGRhdGEgPSBmZWFyb25fc3Vic2V0KQojIHN1bW1hcnkoZGlyZWN0KQoKY29lZnMgPC0gdHJpYmJsZSgKICB+bW9kZWxfbmFtZSwgfm1vZGVsLAogICJCYXNlbGluZSIsIGJhc2VsaW5lLAogICJXaXRoIGluc3RhYmlsaXR5IiwgcHRiaWFzLAogICJGZWFyb24gYW5kIExhaXRpbiIsIGZpcnN0LAogICJBQ0RFIiwgZGlyZWN0KSAlPiUKICBtdXRhdGUodGlkaWZpZWQgPSBtb2RlbCAlPiUgbWFwKH4gdGlkeSguLCBjb25mLmludCA9IFRSVUUpKSkgJT4lCiAgdW5uZXN0KHRpZGlmaWVkKQoKdG9fcGxvdCA8LSBjb2VmcyAlPiUKICBmaWx0ZXIodGVybSA9PSAiZXRoZnJhYyIpICU+JQogIG11dGF0ZShtb2RlbF9uYW1lID0gZmN0X3JldihmY3RfaW5vcmRlcihtb2RlbF9uYW1lKSkpCgpnZ3Bsb3QodG9fcGxvdCwgYWVzKHggPSBlc3RpbWF0ZSwgeSA9IG1vZGVsX25hbWUsIGNvbG9yID0gbW9kZWxfbmFtZSkpICsKICBnZW9tX3BvaW50cmFuZ2VoKGFlcyh4bWluID0gY29uZi5sb3csIHhtYXggPSBjb25mLmhpZ2gpKSArCiAgZ2VvbV92bGluZSh4aW50ZXJjZXB0ID0gMCkgKwogIHNjYWxlX2NvbG9yX3ZpcmlkaXNfZChvcHRpb24gPSAibWFnbWEiLCBlbmQgPSAwLjksIGd1aWRlID0gRkFMU0UpICsKICBsYWJzKHggPSAiRXN0aW1hdGUiLCB5ID0gTlVMTCkgKwogIHRoZW1lX2xpZ2h0KCkKYGBgCgojIyMgT3VyIG93biBhdmVyYWdlIGNvbnRyb2xsZWQgZGlyZWN0IGVmZmVjdCBlc3RpbWF0aW9uCgpJZiB3ZSB3YW50IHRvIGRvIHRoZSBzYW1lIEFDREUgZXN0aW1hdGlvbiwgd2UgaGF2ZSB0byBkaXN0aW5ndWlzaCBiZXR3ZWVuIHRoZXNlIHR5cGVzIG9mIHZhcmlhYmxlczoKCi0gUHJldHJlYXRtZW50IGNvbmZvdW5kZXJzCi0gSW50ZXJtZWRpYXRlIGNvbmZvdW5kZXJzCi0gUG9zdHRyZWF0bWVudCB2YXJpYWJsZXMK
