Why care about causation in nonprofit studies?
Graph and analysis of causal stuff in top 3 here
941 - “Causal empiricism is associated with “identification strategy” research designs.”
This is different from quantitative “pseudo-general pseudo-facts” that come from multiple regression
In quantitative research, pseudo-facts are statistical results that are interpreted erroneously in terms of their causal implications, and pseudo-general findings are ones that are erroneously described as applying to a more general class of units than is immediately warranted.
Don’t make unwarranted causal-ish statements, but also don’t be afraid of the “c-word” (Hernán, 2018)
Language can imply causality even if authors explicitly eschew causal language and identification strategies (Haber et al., 2021-09-03, 2021)
Weasel words - association, determinants, etc. Determinants and prediction is fine! The focus is on getting the most accurate prediction of the outcome When making causal claims, though, the focus is on one of the Xs—one lever that a government agency or nonprofit organization can manipulate to affect some sort of change
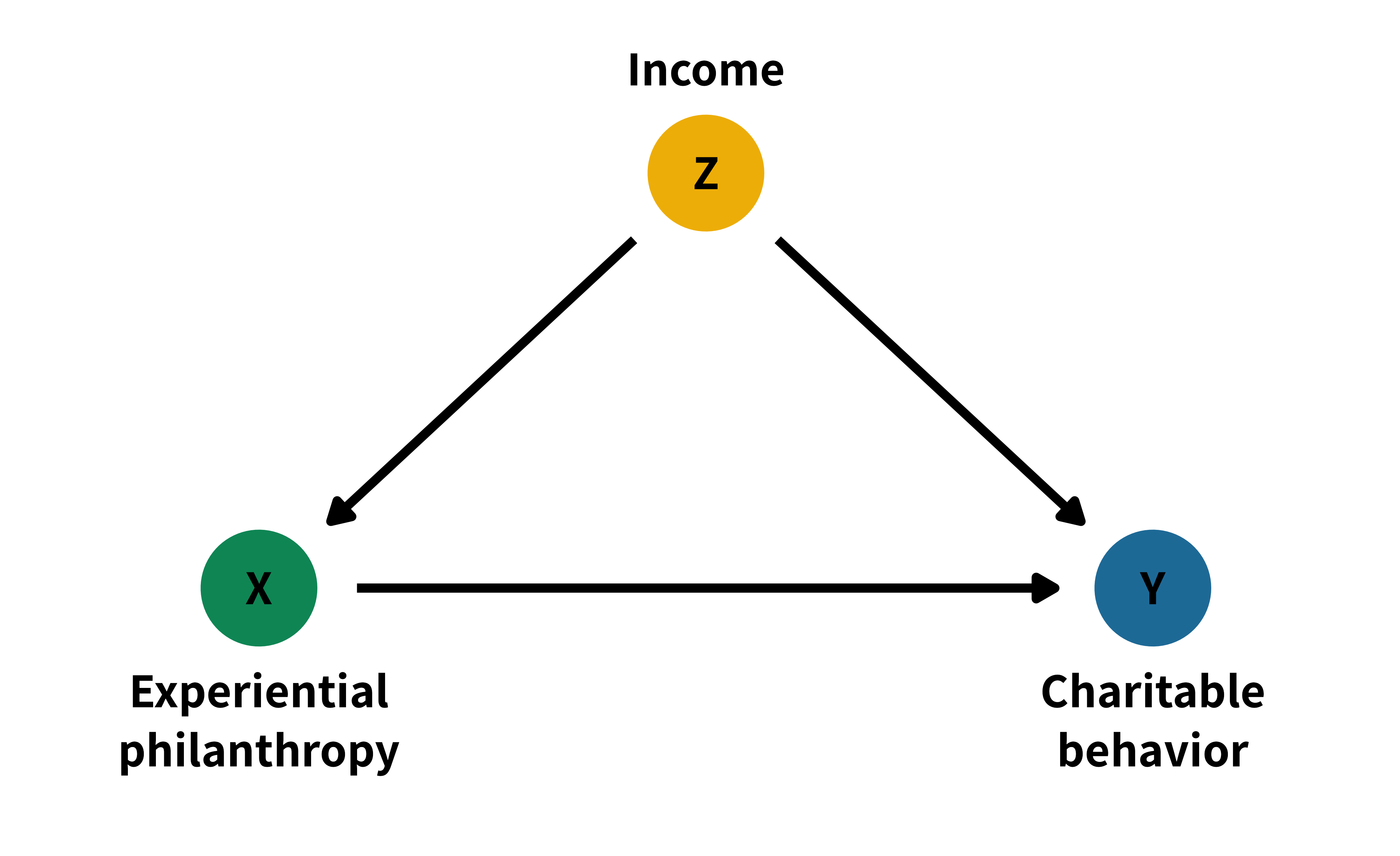
Textbook treatments of causal inference approahces are typically abstract and generic, explaining how treatment \(X\) causes outcome \(Y\) after adjusting for confounders \(Z\). To make these principles as concrete as possible, we use a practical running example relevant to nonprofit education and practice. Experiential philanthropy - Newark, BYU Grantwell and Be a Philanthropist. These programs provide students interested in the nonprofit sector with hands on, practical experience with philanthropy. Beyond their pedagogical aims, these programs are designed to instill a long-term interest and participation in philanthropy.
Do experiential philanthropy programs cause long-term charitable or prosocial behavior?
We do not provide any evidence to answer this question directly. Rather, we use simulated data to explore multiple hypothetical research designs that could be used to quantititavely measure the causal impact of these programs. These causal inference approaches can be applied to a wide range of nonprofit-focued questions, though some methods are better suited than others, depending on the context of the research question. TODO We provide examples of possible nonprofit-related causal inquiries that are amenable to each method
A visual vocabulary for causal inference
Causation through listening
Judea Pearl, computer science, and epidemiology blah blah blah provide us with a specialized framework for describing causal theories and making causal inferences.
At the core of causal inquiry is the notion of “causation,” or what it means when we say that an intervention causes an outcome. In Pearl’s framework, causation can be defined using a metaphor of listening and responding:
A variable \(X\) is a cause of a variable \(Y\) if \(Y\) in any way relies on \(X\) for its value.… \(X\) is a cause of \(Y\) if \(Y\) listens to \(X\) and decides its value in response to what it hears. (Pearl et al., 2016, pp. 5–6).
In the context of our example causal question, we posit that prosocial behavior listens to, responds to, or is caused by experiential philanthropy. We have a theoretical reason to believe that the intervention and the outcome are associated with each other in a sequential, nonspurious way—it is reasonable to assume that having hands-on experience with philanthropy today would influence future attitudes toward charitable giving. Specific educational interventions are not the only cause of prosocial behavior. This behavior listens and responds to other factors, including family background, income, education, and personal attitudes and opinions towards volunteerism and charity—experiential philanthropy is just one of many causes.
Directed acyclic graphs (DAGs)
We can formally represent our theory of how an intervention (\(X\)) causes an outcome (\(Y\)) using a directed acyclic graph, or DAG (Morgan & Winship, 2014; Pearl et al., 2016; Pearl & Mackenzie, 2018). DAGs encode our understanding of the data generating process, or which phenomena cause the treatment, the outcome, and both simultaneously. These causal graphs are a philosophical model of the associations between different phenomena and our assumptions behind those relationships.
- Nodes - nodes can be unmeasurable, or even unobserved
- Edges - Arrows indicate a relationship, or the passing of statistical association between nodes - intervening on one node leads to changes in another node - When two nodes are connected by an arrow, we are stating that there is an assumed causal relationship between those nodes; when there is no arrow between nodes, we are explicitly stating that there is no relationship between the two. Unlike other graphical approaches like structural equation models (SEMs) that assume all relationships are additive and linear, DAG arrows are nonparametric and can represent any kind of functional form (linear, multiplicative, polynomial, exponential, etc.). Accordingly, when we say that \(X \rightarrow Y\), we mean that \(X\) causally affects \(Y\) in some general way, not necessarily linearly (Rohrer, 2018).
- Acyclicity - can’t get back to a node - represents flow of time, or temporal ordering - if things are cyclical, like hiring new staff \(\leftrightarrow\) increased capacity, you can make these nodes time-based: hiring new staff_t → increased capacity_t → hiring new staff_t+1 → increased capacity_t+1
DAGs force researchers to be explicit about their beliefs regarding the relationships between each variable and whether causal relationships do or do not exist (TODO UGH this is a gross sentence)
Importantly, DAGs do more than simply represent the relationships and associations between variables. They provide us with ways to isolate specific relationships of interest. TODO: Rohrer, 28: Even if a researcher does not rely fully on a DAG, mapping out the underlying data-generating process
Statistical associations and causal structures
General explanation of DAGs and confounding/colliding/mediating and d-separation and do-calculus, etc.
This stuff in Figure 2: (Elwert (2013) for forks, chains, inverted forks terminology)
- Confounding - forks
- Mediation - chains
- Collision - inverted forks (Elwert & Winship, 2014; Knox et al., 2020)
Confounding is a major scary issue though - especially if it’s unmeasured or unobservable…
Experiential learning → community connections → long-term pro-social outcomes
Experiential learning → MPA students ← Pro-social behaviors
Collider bias is often seen as a form of selection bias, leading to results that are not generalizable to other contexts. Colliders can lead to bias beyond issues of selection, though. KnoxLoweMummolo use a DAG to argue that police stops, race, administrative records, etc.
Bad controls
Even if we do not rely on a DAG for complete identification of causal effects, mapping out the relationships between nodes in the data-generating process is a useful exercise in any kind of quantitative, regression-based analysis, including non-causal descriptive work. Researchers often take a “kitchen sink” approach to statistical control, including all potential covariates in a model. Understanding the underlying DAG provides clearer guidance about what to control for, helping researchers avoid “bad controls” (cite?). For instance, if a potential covariate is only associated with the outcome and has no relationship to the treatment, it is not a confounder and need not be included as a control variable in a model, since it can reduce the precision of the model estimates. If a potential covariate is a collider, caused by both the treatment and the outcome, the model results will be biased or distorted.
In addition to identification, DAGs provide additional statistical insight and guidance regarding control variables or covariates in regression models
Bad controls and colliders
Good/bad controls: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3689437 - https://twitter.com/analisereal/status/1512596580632707078
Table 2 fallacy + Keele et al. (2020) thing
Post-treatment control bias - cite that one paper by Brendan Nyhan - DAGs make it obvious which nodes are post-treatment, since they appear after the treatment node in the causal chain in the graph
Identifying and isolating causal relationships
Fundamental problem of causal inference
Formulating and testing hypotheses is the foundation of scientific inquiry. In chemistry, researchers can intervene with blah blah H2O
People and individuals, however, do not respond in identical ways. Counterfactuals - what would have happened in the absense of an intervention to the same person or organization.
Rubin notation for individual potential outcomes Treatment effect = whatever
However, it is impossible to observe or measure both Yi0 and Yi1. A charitable foundation interested in poverty reduction cannot give a grant to a nonprofit and simultaneously not give it to the same nonprofit in order to measure the impact of its donation. What the recipient nonprofit receives (or does not receive) from the foundation becomes a realized outcome rather than a potential outcome, and the counterfactual outcome is forever unrealized and unmeasurable.
To get around this, we can take the average (or expectation, often indicated with the mathematical function E) of many units that receive the treatment and compare it with the average of comparable units that don’t receive the treatment
Rubin notation: Potential outcomes notation
To help clarify that blah blah, we’ll introduce one more piece of mathematical notation - the do() operator
Pearl notation: \(\operatorname{do}(x)\) notation = an intervention.
Selection bias
In addition to the fact that potential outcomes are unobservable, one more characteristic of observational data makes causal inference more complicated.
Individuals and organizations have agency and choose their interventions
A foundation interested in reducing poverty will typically research a range of candidate nonprofits and select the one that fits their own internal criteria. Nonprofits applying for a grant from that foundation will tailor their applications to meet the foundation’s preferences. Accordingly, there are systematic differences between nonprofits that receive a grant and those that don’t. It is tempting to measure the average outcome of recipient nonprofits and compare it with the average outcome of non-recipient nonprofits, but this estimate would be incorrect.
Formula showing wrong effect
Causal identification and d-separation
To identify a causal relationship in a DAG, we have to ensure that the arrow between the treatment and outcome nodes is isolated and that the treatment and outcome nodes are not linked through any other pathways
In addition to encoding our philosophy and theory of the data generating process, DAGs also serve as an important statistical tool for isolating or identifying causal quantities of interest. Identification strategy definition:
The central role of an identification strategy is to provide a logic for establishing that D is independent of potential values of Y, thus allowing the analyst to interpret observed associations as causal effects. (Keele et al., 2020)
- d-connection and d-separation - statistical association cannot pass between nodes, either because the arrows are drawn in a way that makes it so information does not link the two, or because conditioning/adjustment blocks the pathway
do-calculus and statistical adjustment
In experiments, the researcher has total control over assignment to treatment, which means all edges/arrows that might influence treatment can be removed. There is no confounding to worry about and we can measure the exact causal effect of X on Y. In potential outcomes language, you still can’t see each individual’s yes and no response, but you can average all the yeses and noes and get an average causal effect
With observational data, we’d like to measure \(\mathbf{E}(y \mid \operatorname{do}(x))\) but we can only actually see and measure \(\mathbf{E}(y \mid x)\), and as shown in Equation 1, these two expressions are not the same. This is a formal statement of the phrase “correlation isn’t causation”:
\[ {\color{gray} \overbrace{{\color{orange} \underbracket[0.25pt]{{\color{black} \mathbf{E}(y \mid \operatorname{do}(x)) \vphantom{\frac{1}{2}}}}_{\color{orange} \text{``Causation"}}}}^{\color{gray} \mathclap{\substack{\text{The average} \\ \text{population-level} \\ \text{change in $y$ when} \\ \textit{directly intervening} \\ \text{(or doing) $x$}}}}} \quad \neq \quad {\color{gray} \overbrace{\color{purple} \underbracket[0.25pt]{{\color{black} \mathbf{E}(y \mid x)} \vphantom{\frac{1}{2}}}_{\color{purple} \text{``Correlation"}}}^{\color{gray} \mathclap{\substack{\text{The average} \\ \text{population-level} \\ \text{change in $y$ when} \\ \text{accounting for} \\ \textit{observed } x}}}} \tag{1}\]
What we want to be able to do is transform the \(\mathbf{E}(y \mid \operatorname{do}(x))\) expression into something without the \(\operatorname{do}(x)\), or something do-free. A set of three systematic rules for analyzing and decomposing causal graphs known as do-calculus provide certain conditions under which we can treat an interventional \(\operatorname{do}(\cdot)\) expression like an observed value instead. A complete exploration of these three rules of do-calculus go beyond the scope of this paper, but lots of resources like Pearl, that one textbook, other things in my blog post, etc. (Pearl, 2012, 2019)
The most common derivation of the rules of do-calculus is an approach called “backdoor adjustment”. By adjusting or controlling for nodes that open up backdoor paths between the treatment and outcome nodes, we can mathematically transform a \(\operatorname{do}(\cdot)\) expression into something based solely on observational data. Formally, the backdoor adjustment formula is defined in Equation 2:
\[ {\color{gray} \overbrace{\color{black} \mathbf{E}(y \mid \operatorname{do}(x)) \vphantom{\frac{1}{2}}}^{\substack{\text{Causal effect} \\ \text{of $x$ on $y$}}}} \quad=\quad {\color{gray} \underbrace{{\color{black} \sum_z}}_{\mathclap{\substack{\text{Sum across} \\ \text{all values of $z$}}}}} {\color{gray} \overbrace{\color{black} \mathbf{E} (y \mid x, z) \vphantom{\frac{1}{2}}}^{\mathclap{\substack{\text{Conditional} \\ \text{mean of $y$,} \\ \text{given $x$ and $z\dots$}}}}} \enspace\times\enspace {\color{gray} \overbrace{\color{black} \mathbf{P}(z) \vphantom{\frac{1}{2}}}^{\mathclap{\substack{\text{$\dots$ weighted} \\ \text{by $z$}}}}} \tag{2}\]
Put more simply, @ref(eq:backdoor) demonstrates that we can remove the interventional \(\operatorname{do}(x)\) from the left-hand side of the equation by controlling for (or conditioning on) all the confounders \(z\) that open up a backdoor pathway between treatment and outcome. As a simplified illustration, suppose that the relationship between treatment and outcome is confounded only by a nonprofit’s size, which is measured as either large or small. Applying this backdoor adjustment formula would entail finding average value of the outcome conditioned on the treatment among large nonprofits, multiplied by the proportion of large nonprofits, added to the average value of the outcome conditioned on the treatment among small nonprofits, multiplied by the proportion of small nonnprofits. The resulting sum would then be the unconfounded causal effect.
In practice, statistical adjustment rarely involves a single binary confounder. For instance, in the causal graph in Fig X, X, Y, and Z all open up backdoors between treatment and outcome, and all three would need to be adjusted for. We will provide a practical demonstration of more common adjustment strategies when there are multiple confounders in section X. At this point, what is important to note is that adjusting for confounding nodes allows us to isolate the single pathway between treatment and outcome. Because spurious statistical associations from other nodes have been blocked statistically, the relationship we care about is identified and we can talk about the causal effect of the treatment on the outcome.
TODO: Plot of backdoor and frontdoor adjustment DAGs, but using nonprofit situations
A less common derivation of the rules of do-calculus is frontdoor adjustment, commonly used when confounding is unobserved and undertheorized and unmeasurable. Smoking genetics tar cancer thing - Bellemare paper example (Bellemare et al., 2020-06-18, 2020) - frontdoor adjustment formula here? We do not provide a complete example here—see Bellemare for that—but again, what is most important here is that we can again mathematically transform a quantity with an interventional do(x) into a do-free quantity, meaning that we can make causal claims from observational data.
The backdoor and frontdoor criteria are the most common applications of do-calculus because they are readily apparent in causal graphs—it is possible to see forks joining exposure and outcome and identify backdoors, or see measurable mediating nodes that could be used as front doors. In more complex DAGs, these backdoor and frontdoor shortcuts might not be readily visible. In that case, there are software packages that algorithmically work through the various rules of do-calculus to determine the set of nodes that need to be adjusted in order to isolate the x → y relationship. Not every DAG is identifiable; but any identifiable DAG can be identified.
The logic of do-calculus tells us what nodes or variables been to be adjusted for to isolate the treatment → outcome arrow, but the DAG provides no guidance about how to actually make these adjustments.
There are two general approaches for doing this:
- Circumstantial identification
- Adjustment-based identification
Circumstantial identification
(Angrist & Pischke, 2009, 2015)
The language of causal graphs, identification, and adjustment provide a universal grammar for discussing causal effects. Commonly used approaches in econometrics and other social science disciplines can be written as causal graphs see 3
RCTs
No need to control for a ton of things in an RCT precisely because the arrows into X get deleted. No need to worry about perfect balance checks because the researcher has control over and understands the data generating process and assignment to treatment. Look at that one knitted Rmd on RCT FAQs: https://macartan.github.io/i/notes/rct_faqs.html - CONSORT also says to stop doing balance tests - only really need to control for things that might be predictive (https://twitter.com/statsepi/status/1115902270888128514?s=21), but theoretically anything that influences the allocation to treatment is taken care of by randomization.
- Explanation + DAG
- Illustration of how to use it
- Review of existing nonprofit studies that use it - survey vignette experiments, conjoint experiments, field experiments, other kinds of RCTs
- Possible nonprofit research questions that could use it
Diff-in-diff + TWFE
Time / location, TWFE stuff
- Explanation + DAG
- Illustration of how to use it
- Review of existing nonprofit studies that use it
- Possible nonprofit research questions that could use it
RDD
Threshold/cutpoint
Adjusting for the threshold and only looking at data right around it makes it so that we can treat the sample as if it were random (by assumption), which then means we can delete any arrows going into X just like an RCT
Cite Nick’s The Effect - refer to his website with the DAGs and animations
- Explanation + DAG
- Illustration of how to use it
- Review of existing nonprofit studies that use it
- Possible nonprofit research questions that could use it
IV
IVs have to meet the exclusion restriction - the instrument can only influence the outcome through the treatment. DAGs make this assumption very clear. There cannot be an arrow connecting the instrument to the outcome. DAGs also inform the exogeneity assumption—no other nodes in the graph can feed into the instrument node
It’s like frontdoor adjustment (https://www.stat.cmu.edu/~cshalizi/402/lectures/23-causal-estimation/lecture-23.pdf) - Really we’re finding the causal effect of I on X, then X on Y, generally through 2SLS
These used to be common, but have become less popular because of the difficulty in finding a valid instrument that meets all the criteria for clean identification. (rainfall-instrument-paper?). Randomized promotion works well, though - (worldbank-book?)
- Explanation + DAG
- Illustration of how to use it
- Review of existing nonprofit studies that use it
- Possible nonprofit research questions that could use it
Adjustment-based identification
Regression adjustment
- Explanation + DAG
- Illustration of how to use it
- Review of existing nonprofit studies that use it
- Possible nonprofit research questions that could use it
IPW and g-computation
- Explanation + DAG
- Illustration of how to use it
- Review of existing nonprofit studies that use it
- Possible nonprofit research questions that could use it
Matching creates entirely new treatment/control populations
IPW creates comparable pseudo populations
MAYBE: Make an image with little shaded people showing how matching and IPW work, similar to Torres:2020 (maybe with https://github.com/propublica/weepeople ?)
Despite its popularity in epidemiology and public health, to our knowledge, there are no studies in NVSQ, Voluntas, or NML that employ inverse probability weighting for covariate adjustment for causal inference. There are X that use matching, and there are many that use regression-based adjustment in explicitly non-causal ways (but Haber et al paper finds that these things imply causation anyway). For instance, Huafang et al. paper explicity talks about associations after controlling for ostensible confounders, but also uses causal language like “program impacts” - C-word article and not shying away from causation
Hybrid approaches
Briefly describe combinations of the two approaches, like synthetic controls, DiD with matching, RDD with covariate adjustment, etc.
Briefly mention other methods, like marginal structural models (Blackwell & Glynn, 2018)?
Tools for researchers and practitioners
Code in R and Stata? Point to other resources like The Mixtape, The Effect, Pearl’s stuff, Morgan and Winship?
Conclusion
A call for more causation / more careful thinking around causation. Prediction is fine. But don’t automatically run away from causal work.
We believe that adjustment-based approaches like regression adjustment, matching, and IPW are highly amenable to nonprofit administrative data. Finding specific situations like diff-in-diff is popular in public policy analysis and econometrics because the scale of the data is much larger—researchers can analyze the effect of state- or national-level policies in difference-in-difference designs, or observe the behavior of millions of participants in programs like Medicaid or the Affordable Care Act for regression discontinuity designs. A smaller nonprofit interested in evaluating the impact of a new community program is most likely unable to consider these types of situation-specific quasi-experimental designs to isolate the causal effect. However, with careful theoretical thinking; the development of a robust DAG that describes potential confounders, mediators, and colliders; the use of high quality administrative data; and intentional sensitivity analysis that probes the strength of possible causal relationships when faced with unmeasured confounding (that-sensmakr-paper?; lucys-tipr-paper?); nonprofit researchers can tell plausible causal stories.
References
Angrist, J. D., & Pischke, J.-S. (2009). Mostly Harmless Econometrics: An Empiricist’s Companion. Princeton University Press.
Angrist, J. D., & Pischke, J.-S. (2015). Mastering ’Metrics: The Path from Cause to Effect. Princeton University Press.
Ba, Y., Berrett, J., & Coupet, J. (2021). Panel Data Analysis: A Guide for Nonprofit Studies. Voluntas: International Journal of Voluntary and Nonprofit Organizations, 1–16. https://doi.org/10.1007/s11266-021-00342-w
Bellemare, M. F., Bloem, J. R., & Wexler, N. (2020-06-18, 2020). The Paper of How: Estimating Treatment Effects Using the Front-Door Criterion [Working paper]. http://marcfbellemare.com/wordpress/wp-content/uploads/2020/06/BellemareBloemWexlerFDCJune2020.pdf
Blackwell, M., & Glynn, A. N. (2018). How to Make Causal Inferences with Time-Series Cross-Sectional Data under Selection on Observables. American Political Science Review, 112(4), 1067–1082. https://doi.org/10.1017/s0003055418000357
Cunningham, S. (2021). Causal Inference: The Mixtape. Yale University Press. https://mixtape.scunning.com/
Elwert, F. (2013). Graphical Causal Models. In S. L. Morgan (Ed.), Handbook of Causal Analysis for Social Research (pp. 245–273). Springer. https://doi.org/10.1007/978-94-007-6094-3_13
Elwert, F., & Winship, C. (2014). Endogenous Selection Bias: The Problem of Conditioning on a Collider Variable. Annual Review of Sociology, 40, 31–53. https://doi.org/10.1146/annurev-soc-071913-043455
Haber, N. A., Wieten, S. E., Rohrer, J. M., Arah, O. A., Tennant, P. W. G., Stuart, E. A., Murray, E. J., Pilleron, S., Lam, S. T., Riederer, E., Howcutt, S. J., Simmons, A. E., Leyrat, C., Schoenegger, P., Booman, A., Dufour, M.-S. K., O’Donoghue, A. L., Baglini, R., Do, S., … Fox, M. P. (2021-09-03, 2021). Causal and Associational Linking Language From Observational Research and Health Evaluation Literature in Practice: A Systematic Language Evaluation. medRxiv : The Preprint Server for Health Sciences. https://doi.org/10.1101/2021.08.25.21262631
Hernán, M. A. (2018). The C-Word: Scientific Euphemisms Do Not Improve Causal Inference From Observational Data. American Journal of Public Health, 108(5), 616–619. https://doi.org/10.2105/AJPH.2018.304337
Huntington-Klein, N. (2021). The Effect: An Introduction to Research Design and Causality. Chapman and Hall / CRC. https://theeffectbook.net/
Keele, L., Stevenson, R. T., & Elwert, F. (2020). The Causal Interpretation of Estimated Associations in Regression Models. Political Science Research and Methods, 8(1), 1–13. https://doi.org/10.1017/psrm.2019.31
Knox, D., Lowe, W., & Mummolo, J. (2020). Administrative Records Mask Racially Biased Policing. American Political Science Review, 114(3), 619–637. https://doi.org/10.1017/S0003055420000039
Ma, J., Ebeid, I. A., de Wit, A., Xu, M., Yang, Y., Bekkers, R., & Wiepking, P. (2023). Computational Social Science for Nonprofit Studies: Developing a Toolbox and Knowledge Base for the Field. VOLUNTAS: International Journal of Voluntary and Nonprofit Organizations, 34(1), 52–63. https://doi.org/10.1007/s11266-021-00414-x
Morgan, S. L., & Winship, C. (2014). Counterfactuals and Causal Inference: Methods and Principles for Social Research (2nd ed.). Cambridge University Press. https://doi.org/10.1017/cbo9781107587991
Pearl, J. (2012). The Do-Calculus Revisited. Proceedings of the Twenty-Eighth Conference on Uncertainty in Artificial Intelligence, 3–11. https://dl.acm.org/doi/10.5555/3020652.3020654
Pearl, J. (2019). On the Interpretation of do(x). Journal of Causal Inference, 7(1), 1–6. https://doi.org/10.1515/jci-2019-2002
Pearl, J., Glymour, M., & Jewell, N. P. (2016). Causal Inference in Statistics: A Primer. Wiley.
Pearl, J., & Mackenzie, D. (2018). The Book of Why: The New Science of Cause and Effect. Basic Books.
Rohrer, J. M. (2018). Thinking Clearly About Correlations and Causation: Graphical Causal Models for Observational Data. Advances in Methods and Practices in Psychological Science, 1(1), 27–42. https://doi.org/10.1177/2515245917745629
Samii, C. (2016). Causal Empiricism in Quantitative Research. Journal of Politics, 78(3), 941–955. https://doi.org/10.1086/686690